先说一些题外话
其实很早就有这些这个的欲望了。。。
但是由于种种原因(包括班主任),一直咕到现在。。。
咕咕咕。。。
不能再咕下去了!
于是熬夜来写这个。
步入正题
先看一个例题:BZOJ1568: [JSOI2008]Blue Mary开公司
其实这个算是裸题了。。。
当然我做的第一道李超树的题不是这个。。。
题目要求区间内的所有直线的最高点的最大值。
并且带插入。
裸的暴力$O(nm)$对吧。
然后呢?
第一想法是——分治!
将一个区间$[l,r]$分成$[l,mid],[mid+1,r]$两个区间,递归求解。
合并答案就取最大值就好。
这样,我们便得出来一个$O(mnlog_2n)$的算法。。。
你会说:“这个算法复杂度还没暴力跑得快,我要他干嘛???”
诚然,暴力跑得比它快得多。。。
但是你觉得这个算法如果没有用的话,我会讲它吗?
我们回头看我们分治的过程:将区间一分为二,且区间大小相等。
如果你有像我一样的超高的$DS$水平,你就会发现这个过程和某个数据结构的过程好像啊!
没错!这个数据结构就是——线段树!
是不是很厉害!
为什么?因为我们找到了一种数据结构来维护这玩意了!
所以线段树每个点存区间最大值就好。
$BUT$!这么做还有一个问题:插入线段怎么办?
你会想:用最大值覆盖不就好了?
那么问题又来了:线段是有斜率的。
也就是说,在不同的点,线段的函数值是不同的。
你怎么知道当前的点的函数值是多少呢?
可能你又会想:那我就暴力带值进线段,把函数值算出来不就好了?
那么恭喜,你离深渊越来越近了。
你会发现你的每一次维护都会涉及到最多$4n$个节点。
那和暴力有什么区别???
所以这个方案被我们舍弃了。
那怎么办呢?
对于这个问题,国家队队爷李超提出一种解决办法:
我们把线段树中存的值从区间最大值改为区间中值最大的直线。
每个节点至少会存一条直线。
但是多条直线呢?
我们可以打一个标记,说明再这个区间内至少有一个两条直线的转折点。
然后递归插入直线。
具体做法是这样的:
假设原来在$[l,r]$这个区间内只有一条直线$f_1(x)=k_1x+b_1$。
现在要在区间内插入一条新直线$f_2(x)=k_2x+b_2$。
然后便是分类讨论:
1. 如果$f_1(l)geq f_2(l),f_1(r)geq f_2(r)$:
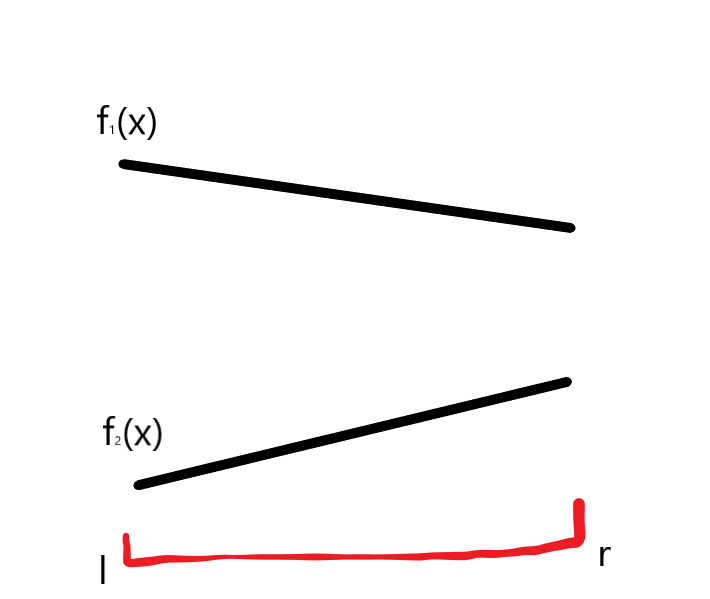
说明$f_2(x)$在这个区间内被$f_1(x)$吊打,那么不做任何操作;
2. 如果$f_1(l)leq f_2(l),f_1(r)leq f_2(r)$:

说明$f_1(x)$在这个区间内被$f_2(x)$吊打,那么直接替换即可;
3. 如果$f_1(l)geq f_2(l),f_1(r)leq f_2(r) ext{或者}f_1(l)leq f_2(l),f_1(r)geq f_2(r)$:
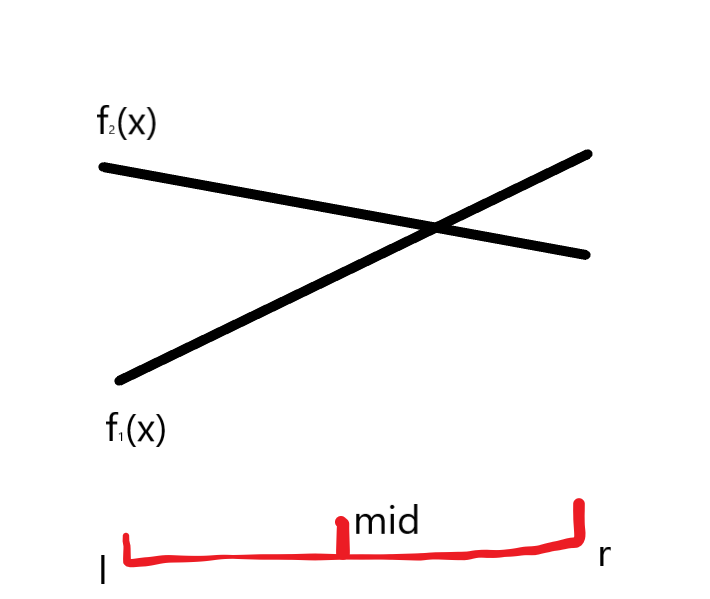
说明两直线在这个区间内有交点。
这时,我们取区间中点$mid$,判断两直线在$[l,mid]$之间是否相交:
若是,则右区间$[mid+1,r]$赋为在上方的曲线,左区间递归求解;
否则,左区间$[l,mid]$赋为在上方的曲线,右区间递归求解。
这样,我们的一次插入直线操作完成。
而递归修改最多会涉及到$log_2n$个节点。
所以一次修改的复杂度上限为$O(log_2^2n)$。
然后,这题还需要用到标记永久化。
即我们不下传标记,在求区间最大值的时候,每次访问到一个被询问区间包含的区间,把答案和这个区间所维护的线段的最大值取$max$。
然后这个题就做完了。
不得不说非常的机智啊!
所以这种线段树被称为——李超树。
复杂度$O(mlog_2^2n)$。
疯狂维护半平面交。。。
代码的话。。。可以去题解里找:
BZOJ1568: [JSOI2008]Blue Mary开公司
再推荐两道练手题:
类似的板子题:
BZOJ3165: [Heoi2013]Segment
我做的第一道李超树题:(万事开头难。。。)
BZOJ4515: [Sdoi2016]游戏
后记
其实李超树不建议在考场上写。
因为这玩意的修改很容易写炸。。。
并且查错及其恶心。。。
对于大多数$DS$能力不是极其强悍的$OIer$来说,性价比并不是很高。
因为一般这种题的部分分都比正解的性价比高。。。
所以不是队爷不写正解。。。
而对于我这个菜鸡$AFO$选手来说,可以浪一浪。。。
出题人,我劝你善良。。。