dfs序与树链剖分
还是先安利一发AgOH https://space.bilibili.com/120174936
模板题:洛谷 P3384 【模板】轻重链剖分
https://www.luogu.com.cn/problem/P3384
如题,已知一棵包含 N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作 1: 格式: 1 x y z 表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
操作 2: 格式: 2 x y 表示求树从 x 到 y 结点最短路径上所有节点的值之和。
操作 3: 格式: 3 x z 表示将以 x 为根节点的子树内所有节点值都加上 z。
操作 4: 格式:4 x 表示求以 x 为根节点的子树内所有节点值之和。
先说dfs序
dfs序,就是dfs的顺序
如图,标记的数字的顺序就是dfs序
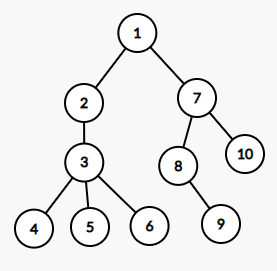
再就是,要区分一下dfs序和欧拉序
dfs序是以深度优先搜索的原则遍历图中节点出现的顺序 --->一个节点只出现一次 1,2,3,4,5,6,7,8,9,10
欧拉序是每经过一次节点,就要把他写出来,如图那就应该是1,2,3,4,3,5,3,6,3,2,1,7,8,9,8,7,10
时间戳
时间戳即dfs第一次访问到每个节点的时间,从1开始递加
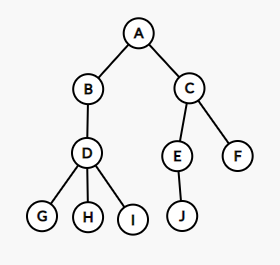
与上面的图对应,我们称A的时间戳为1,D的时间戳为3,E的时间戳为8
Q:那我们搞这个时间戳是用来干嘛的??
A:我们把树搞成了连续的,方便后续对树进行一些操作(暗指线段树 树状数组啥的QAQ)
我们会发现两个重要的性质:
1一个结点的子树上的结点的时间戳,一定大于这个结点的时间戳且连续
2某些链上的时间戳也是连续的
有了上面的性质,操作3和操作4就可以解决了
把树看成是数组,时间戳是下标 tree[1]='A',tree[2]='B……
操作3:将以x为根结点的子树内所有结点值都加上z ---->区间修改 [x,x+子树的大小]
操作4:求以x为根节点的子树内所有结点值的和--->区间查询 [x,x+子树的大小]
树链剖分
那操作1和操作2呢?
树链剖分:把树拆成若干条不相交的链,可以优化一些 树上路径修改及路径信息查询等问题
本质上,树链剖分是一种将树肢解成链平摊开来,再使用线段树对其进行维护的神奇算法
重链剖分O(logn)
长链剖分O(sqrt(n))
实链剖分(搞LCT)
在这我们先考虑更常用的重链剖分
一些术语:
重儿子:一个结点的所有儿子里最重的一个(只有一个也必须有一个,如果一样重随便找一个)
轻儿子:除了重儿子的所有儿子
重链:从一个轻儿子开始(根节点也算)一路往重儿子走连出的一条链
轻链:除了重链的所有链
下面是我们剖好的树
像这样一棵树,紫色结点为重儿子,紫线连成的链就是重链
紫线两端的结点都属于重链
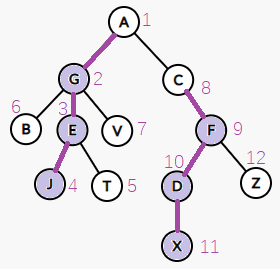
我们之前提到,这样的树上的某些链上的时间戳是连续的,那我们规定优先往重儿子走了之后,这个某些链就成了重链
至于有什么用,继续往下看:
开始剖分
第一遍dfs:标记
1 结点的父亲 fa[maxn]
2 结点的重儿子 son[maxn]
3 结点的深度 deep[maxn]
4 结点的大小 siz[maxn]
第二遍dfs:标记
1 dfs序和时间戳 (结点权值的dfs序 w[maxn])( 时间戳 dfn[maxn])
2 当前结点所在重链的头头是谁(就那个最上面的轻儿子),头的头是他自己 top[maxn]
还需要计数器tim,维护w的线段树,v[maxn]存放所有节点的权值
void dfs1(int u,int f) { fa[u]=f; deep[u]=deep[f]+1;//deep up up siz[u]=1; int maxsize=-1;//find the weight son for(int i=head[u];~i;i=edge[i].next) { int v=edge[i].to; if(v==f) continue;//don't need the father dfs1(v,u);// v is son, u is father siz[u]+=siz[v]; if(siz[v]>maxsize) { maxsize=siz[v]; son[u]=v; } } } void dfs2(int u,int t) { dfn[u]=++tim; top[u]=t; w[tim]=v[u];//Store the value of the current node in its timestamp array if(!son[u]) return ;// can't find the son/the heaviest son dfs2(son[u],t);// first -> the heaviest son for(int i=head[u];~i;i=edge[i].next) { int v=edge[i].to; if(v==fa[u]||v==son[u]) continue;//father or the heaviest son dfs2(v,v);// not the the heaviest son , the light son is himself } }
操作三和操作四
inline void mson(int x,int z) {//将以x为根节点的子树内所有节点值都加上z modify(dfn[x],dfn[x]+siz[x]-1,z); } inline int qson(int x) {//求以x为根节点的子树内所有节点值的和 return query(dfn[x],dfn[x]+siz[x]-1); }
树链剖分找LCA
先来证明一个定理:除根结点外的任何一个结点的父亲结点都一定在一条重链上
证明:因为父亲结点存在儿子,所以一定存在重儿子,所以-一定在一条重链上
操作一和操作二
操作 1: 格式: 1 x y z 表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
操作 2: 格式: 2 x y 表示求树从 x 到 y 结点最短路径上所有节点的值之和。

不难发现,任何一条路径都是由重链的一部分和叶子节点组成
如果要查询的两个结点在同一条重链上,那直接在线段树上查询就好了
如果不在一条重链上,那我们可以考虑把所在重链的top深度大的那个点跳到top处,顺便利用线段树区修,再把top跳到top的父亲,因为之前的那个定理,所以一直循环这个操作,是保证有解的,连续套娃,直到两个数跳到了同一结点或同一深度,over
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 #define lowbit(a) ((a)&-(a)) 5 #define clean(a,b) memset(a,b,sizeof(a)) 6 const int inf=0x3f3f3f3f; 7 const int maxn = 1e5+10; 8 const int maxm=maxn*2; 9 int _,mod; 10 11 ///////////////////////////////////////////////////////////////////////////////////////// 12 struct node 13 { 14 int l,r,sum,add; 15 }tree[maxn*4]; 16 int tim,v[maxn],w[maxn];// w -> the node's dfs xu 17 int fa[maxn],deep[maxn],siz[maxn],son[maxn]; 18 int dfn[maxn],top[maxn]; 19 /*********************************链式前向星************************************/ 20 struct E 21 { 22 int to,next; 23 }edge[maxm]; 24 int tot,head[maxn]; 25 inline void addedge(int u,int v) 26 { 27 edge[tot]=(E){v,head[u]}; 28 head[u]=tot++; 29 edge[tot]=(E){u,head[v]}; 30 head[v]=tot++; 31 } 32 /********************************树链剖分大法************************************/ 33 void dfs1(int u,int f) 34 { 35 fa[u]=f; 36 deep[u]=deep[f]+1;//deep up up 37 siz[u]=1; 38 int maxsize=-1;//find the weight son 39 for(int i=head[u];~i;i=edge[i].next) 40 { 41 int v=edge[i].to; 42 if(v==f) continue;//don't need the father 43 dfs1(v,u);// v is son, u is father 44 siz[u]+=siz[v]; 45 if(siz[v]>maxsize) 46 { 47 maxsize=siz[v]; 48 son[u]=v; 49 } 50 } 51 } 52 void dfs2(int u,int t) 53 { 54 dfn[u]=++tim; 55 top[u]=t; 56 w[tim]=v[u];//Store the value of the current node in its timestamp array 57 if(!son[u]) return ;// can't find the son/the heaviest son 58 dfs2(son[u],t);// first -> the heaviest son 59 for(int i=head[u];~i;i=edge[i].next) 60 { 61 int v=edge[i].to; 62 if(v==fa[u]||v==son[u]) continue;//father or the heaviest son 63 dfs2(v,v);// not the the heaviest son , the light son is himself 64 } 65 } 66 /*******************************线段树*******************************************/ 67 void push_up(int now) 68 { 69 tree[now].sum=(tree[now<<1].sum+tree[now<<1|1].sum)%mod; 70 } 71 void push_down(int now) 72 { 73 tree[now<<1].sum+=(tree[now<<1].r-tree[now<<1].l+1)*tree[now].add; 74 tree[now<<1|1].sum+=(tree[now<<1|1].r-tree[now<<1|1].l+1)*tree[now].add; 75 tree[now<<1].sum%=mod; 76 tree[now<<1|1].sum%=mod; 77 tree[now<<1].add+=tree[now].add; 78 tree[now<<1|1].add+=tree[now].add; 79 tree[now].add=0; 80 } 81 void build(int l,int r,int now=1) 82 { 83 tree[now].l=l; 84 tree[now].r=r; 85 tree[now].add=0; 86 if(l==r) 87 { 88 tree[now].sum=w[l]%mod; 89 return ; 90 } 91 int mid=(l+r)>>1; 92 build(l,mid,now<<1); 93 build(mid+1,r,now<<1|1); 94 push_up(now); 95 } 96 void modify(int l,int r,int k,int now=1) 97 { 98 if(l==tree[now].l&&r==tree[now].r) 99 { 100 tree[now].sum+=(r+1-l)*k; 101 tree[now].sum%=mod; 102 tree[now].add+=k; 103 return ; 104 } 105 if(tree[now].add) push_down(now); 106 int mid=(tree[now].l+tree[now].r)>>1; 107 if(r<=mid) modify(l,r,k,now<<1); 108 else if(l>mid) modify(l,r,k,now<<1|1); 109 else 110 { 111 modify(l,mid,k,now<<1); 112 modify(mid+1,r,k,now<<1|1); 113 } 114 push_up(now); 115 } 116 int query(int l,int r,int now=1) 117 { 118 if(l==tree[now].l&&r==tree[now].r) 119 { 120 return tree[now].sum; 121 } 122 if(tree[now].add) push_down(now); 123 int mid=(tree[now].l+tree[now].r)>>1; 124 int sum=0; 125 if(r<=mid) sum+=query(l,r,now<<1); 126 else if(l>mid) sum+=query(l,r,now<<1|1); 127 else 128 { 129 sum+=query(l,mid,now<<1)+query(mid+1,r,now<<1|1); 130 } 131 return sum%mod; 132 } 133 /*******************************操作****************************************/ 134 135 void mchain(int x,int y,int z) 136 {//将树从 x 到 y 结点最短路径上所有节点的值都加上 z 137 z%=mod; 138 while(top[x]!=top[y])//不在一条重链上 139 { 140 if(deep[top[x]]<deep[top[y]]) 141 { 142 swap(x,y); 143 }//保证x的深度最大,每次都把x跳上去 144 modify(dfn[top[x]],dfn[x],z); 145 x=fa[top[x]]; 146 }//此时他俩一定是在一条重链上的 147 if(deep[x]>deep[y]) swap(x,y); 148 modify(dfn[x],dfn[y],z); 149 } 150 int qchain(int x,int y) 151 { 152 int ret=0; 153 while(top[x]!=top[y]) 154 { 155 if(deep[top[x]]<deep[top[y]]) 156 { 157 swap(x,y); 158 }//保证x的深度最大,每次都把x跳上去 159 ret+=query(dfn[top[x]],dfn[x]); 160 x=fa[top[x]]; 161 } 162 if(deep[x]>deep[y]) swap(x,y); 163 ret+=query(dfn[x],dfn[y]); 164 return ret%mod; 165 } 166 inline void mson(int x,int z) 167 {//将以x为根节点的子树内所有节点值都加上z 168 modify(dfn[x],dfn[x]+siz[x]-1,z); 169 } 170 inline int qson(int x) 171 {//求以x为根节点的子树内所有节点值的和 172 return query(dfn[x],dfn[x]+siz[x]-1); 173 } 174 ///////////////////////////////////////////////////////////////////////////////////////// 175 176 int main() 177 { 178 clean(head,-1); 179 int n,m,r; 180 scanf("%d%d%d%d",&n,&m,&r,&mod); 181 for(int i=1;i<=n;i++) scanf("%d",&v[i]); 182 for(int i=1;i<n;i++) 183 { 184 int u,v; 185 scanf("%d%d",&u,&v); 186 addedge(u,v); 187 } 188 dfs1(r,r); 189 dfs2(r,r); 190 build(1,n); 191 while(m--) 192 { 193 int num,x,y,z; 194 scanf("%d",&num); 195 switch(num) 196 { 197 case 1: 198 scanf("%d%d%d",&x,&y,&z); 199 mchain(x,y,z); 200 break; 201 202 case 2: 203 scanf("%d%d",&x,&y); 204 printf("%d ",qchain(x,y)); 205 break; 206 207 case 3: 208 scanf("%d%d",&x,&z); 209 mson(x,z); 210 break; 211 212 case 4: 213 scanf("%d",&x); 214 printf("%d ",qson(x)); 215 break; 216 } 217 } 218 return 0; 219 }