线索二叉树原理
一个有n个结点的二叉链表,每个结点有指向左右孩子的两个指针域,所以一共有2n个指针域。而n个结点的二叉树一共有n - 1条分支线,也就是说,其实存在2n - ( n - 1 ) = n + 1 个空指针域。
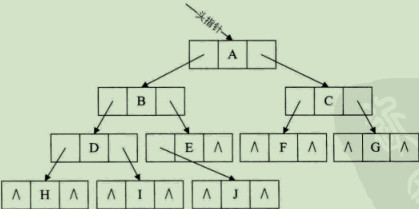 如图10个结点,而空指针域为11
如图10个结点,而空指针域为11
利用这些空地址,存放指向结点在某种遍历次序下的前驱和后继的地址。把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索二叉链表,相应的二叉树就称为为线索二叉树(Threaded Binary Tree)。
我们把这颗二叉树进行中序遍历后,将所有的空指针域中的rchild,改为指向它的后继结点。于是我们就可以通过指针知道H的后继是D(图中1),I的后继是B,J的后继是E,E的后继是A,F的后继是C,G的后继因为不存在而指向NULL。此时共有6个空指针域被利用。
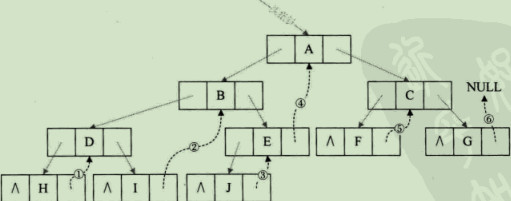
我们再将这颗二叉树的所有空指针域的lchild改为指向当前结点的前驱。因此H的前驱是NULL(图中1),I的前驱是D(图中2),J的前驱是B,F的前驱是A,G的前驱是C。一共5个空指针域被利用,正好和上面的后继加起来11个。
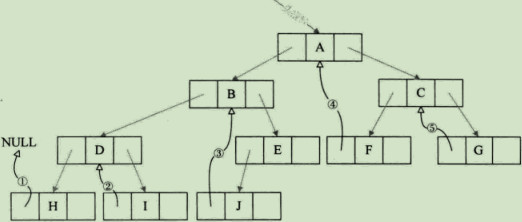
如下图(空心箭头实线为前驱,虚线黑箭头为后继),更容易看出,其实线索二叉树等于把一颗二叉树转变成了一个双向链表,这样对我们的插入删除查找某个结点都带来了方便。所以我们对二叉树以某种次序遍历使其变为线索二叉树的过程称作是线索化。

好事多磨,如何知道某一结点的lchild是指向它的左孩子还是指向前驱? rchild是指向右孩子还是指向后继?
我们增设两个标志域ltag和rtag,注意ltag和rtag只是存放0或1数字的布尔型变量,其占用的内存空间要小于像lchild和rchild的指针变量。
结点结构如图:
其中:
1.ltag为0时指向该结点的左孩子,为1时指向该结点的前驱。
2.rtag为0时指向该结点的右孩子,为1时指向该结点的后继。
因此可将上序二叉链表修改成下图:
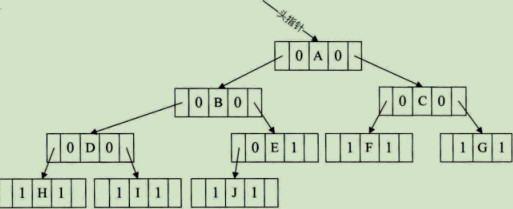
线索二叉树结构实现
二叉树的二叉线索存储结构定义代码如下:
typedef enum {Link,Thread}PointerTag; //Link==0表示指向左右孩子指针 //Thread==1表示指向前驱或后继的线索 typedef struct BiThrNode { char data; struct BiTNode *lchild, *rchild; //左右孩子指针 PointerTag LTag; PointerTag RTag; //左右标志 }BiThrNode,*BiThrTree;
线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。
由于前驱和后继的信息只有在遍历该二叉树时才能得到,所以线索化的过程就是在遍历的过程中修改空指针的过程。
中序遍历线索化的递归函数代码如下:
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点 //中序遍历进行中序线索化 void InThreading(BiThrTree p) { if (p) { InThreading(p->lchild); //递归左子树线索化 if (!p->lchild) //没有左孩子 { p->LTag = Thread; //前驱线索 p->lchild = pre; //左孩子指针指向前驱 } if (!pre->rchild) //前驱没有右孩子 { pre->RTag = Thread; //后继线索 pre->rchild = p; //前驱右孩子指针指向后继(当前结点p) } pre = p; //保持pre指向p的前驱 InThreading(p->rchild); //递归右子树线索化
if(!p->lchild)表示如果某结点的左指针域为空,因为其前驱结点刚刚访问过,赋值给了pre,所以可以将pre赋值给p->lchild,并修改
p->LTag = Thread(也就是定义为1)以完成前驱结点的线索化。
后继就要麻烦一些。因为此时p结点的后继还没有访问到,因此只能对它的前驱结点pre的右指针rchild左判断,if(!pre->rchild)表示如果为空,则p就是Pre的后继,于是pre->rchild=p,并且设置pre->RTag=Thread,完成后续结点的线索化。
完成前驱和后继的判断后,别忘记将当前的结点p赋值给pre,以便下一次使用。
有了线索二叉树后,我们对它进行遍历时发现,其实就等于是操作一个双向链表结构。和双向链表结构一样,在二叉树线索链表上添加一个头结点,如图示:
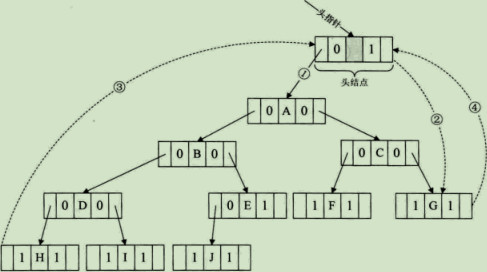
并令lchild域的指针指向二叉树的根结点(图中的1),其rchild域的指针指向中序遍历时访问的最后一个结点(图中的2)。反之,令二叉树的中序序列中的第一个结点中的lchild域指针和最后一个结点rchild域指针均指向头结点(图中的2和4)。这样定义的好处就是我们既可以从第一个结点起顺序后继进行遍历,也可以从最后一个结点其顺前驱进行遍历。
遍历代码如下:
typedef enum {Link,Thread}PointerTag; //Link==0表示指向左右孩子指针 //Thread==1表示指向前驱或后继的线索 typedef struct BiThrNode { char data; struct BiTNode *lchild, *rchild; //左右孩子指针 PointerTag LTag; PointerTag RTag; //左右标志 }BiThrNode,*BiThrTree; BiThrTree pre; //全局变量,始终指向刚刚访问过的结点 //T指向头结点,头结点左链lchild指向根结点 //头结点右链rchild指向中序遍历的最后一个结点
//中序遍历 二叉线索链表表示的二叉树T void InOrderTraverse_Thr(BiThrTree T) { BiThrTree p; p = T->lchild; //p指向根结点 while (p != T) { while (p->LTag == Link) //循环到中序序列第一个结点 p = p->lchild; printf("%c", p->data); //显示结点数据,可以更改为其它对结点的操作 while (p->RTag == Thread&&p->rchild != T) { p = p->rchild; printf("%c", p->data); } p = p->data; //p进至右子树的根 } }
从这段代码可以看出,它等于一个链表的扫描,所以时间复杂度为O(n)。