一、定义:
树(Tree):是n (n>=0)个结点的有限集。
当n=0时 (根节点是唯一的),称为空树。在任意一个非空树中:1)有且仅有一个特定的称为根(Root)的结点;2)当 n > 1 时,其余结点可以分为m (m>0) 个互不相交的有限集T1、T2...、Tm,其中每一个集合本身又是一颗树,并且称为根的子树(SubTree)。
二、结点分类
树(Tree)的结点包含一个数据元素系若干指向其子树的分支。
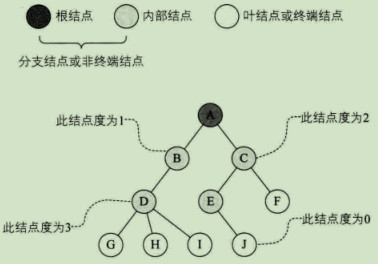
度:结点拥有的子树数称为结点的度。树的度是树内各结点的度的最大值。
叶结点(Left)或终端结点:度为0的结点。
分支结点或非终端结点:度不为0的结点。除根结点之外,分支结点也称为内部结点。
三、结点间关系
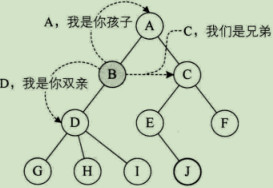
结点的子树的根称为该结点的孩子, 相应地,该结点称为孩子的双亲结点。
同一个双亲的孩子之间互称兄弟(Sibling)。
结点的祖先是从根到该结点所经分支上的所有结点。所以对H来说,D、B、A、都是它的祖先。
相反,以某结点为根的子树中任一结点都称为该结点的子孙。B的子孙有D、G、H、I,如图所示:
四、树的层次关系
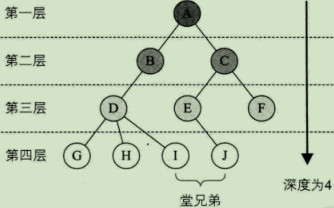
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。
其双亲在同一层的结点互为堂兄弟。
树中结点的最大层次称为树的深度(Depth)或高度。
有序树和无序树
如果将树中结点的各子树看成从左到右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
森林(Forest)是m(m > 0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
树和线性表的区别
1、线性表: 2、树:
第一个数据元素:无前驱 根结点:无双亲,唯一
最后一个数据元素:无后继 叶结点:无孩子,一棵树可以有多个叶结点
中间元素:一个前驱一个后继 中间结点:一个双亲,可以有多个孩子