Description
小胖最近迷上了3D物体,尤其是立方体。他手里有很多个立方体,他想让所有的立方体全都长得一样,所以他决定给某些立方体的表面重涂颜色,使得所有的立方体完全相同。但是小胖是很懒的,他想知道最少涂多少次颜色,可以让所有立方体完全相同。
Input
输入包含多组数据,每组数据第一行n(1<=n<=4),表示立方体的数量,接下来n行,每行6个字符串,表示立方体6个面的颜色:Color 1 Color 2 Color 3 Color 4 Color 5 Color 6,中间用一个空格隔开。
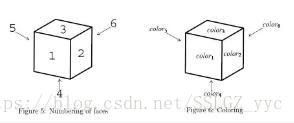
其中,面的标号如下:
n=0表示输入结束。
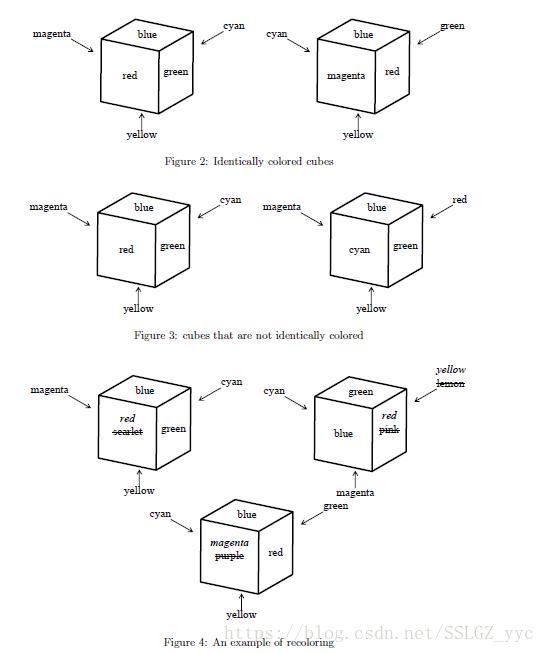
两个立方体被视为相同,当且仅当他们可以在某种摆放方式下,每个面的颜色都对应相同。
一种涂色的方案如下:
Output
每组数据,输出一行一个整数,表示最少的涂色数。(涂一个面算一次涂色)
Sample Input
3
scarlet green blue yellow magenta cyan
blue pink green magenta cyan lemon
purple red blue yellow cyan green
2
red green blue yellow magenta cyan
cyan green blue yellow magenta red
2
red green gray gray magenta cyan
cyan green gray gray magenta red
2
red green blue yellow magenta cyan
magenta red blue yellow cyan green
3
red green blue yellow magenta cyan
cyan green blue yellow magenta red
magenta red blue yellow cyan green
3
blue green green green green blue
green blue blue green green green
green green green green green sea-green
3
red yellow red yellow red yellow
red red yellow yellow red yellow
red red red red red red
4
violet violet salmon salmon salmon salmon
violet salmon salmon salmon salmon violet
violet violet salmon salmon violet violet
violet violet violet violet salmon salmon
1
red green blue yellow magenta cyan
4
magenta pink red scarlet vermilion wine-red
aquamarine blue cyan indigo sky-blue turquoise-blue
blond cream chrome-yellow lemon olive yellow
chrome-green emerald-green green olive vilidian sky-blue
0
Sample Output
4
2
0
0
2
3
4
4
0
16
.
.
.
.
.
.
分析
首先写出正方体有24个旋转方式,然后以第一个正方体为标准,枚举剩下n - 1个正方体的状态,然后计算最小值。
.
.
.
.
.
.
程序:
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
char name[30][30];
int n,ans,tj,c[30],s[30][30];
const int kn[24][6]=
{
{2, 1, 5, 0, 4, 3},{2, 0, 1, 4, 5, 3},{2, 4, 0, 5, 1, 3},{2, 5, 4, 1, 0, 3},
{4, 2, 5, 0, 3, 1},{5, 2, 1, 4, 3, 0},{1, 2, 0, 5, 3, 4},{0, 2, 4, 1, 3, 5},
{0, 1, 2, 3, 4, 5},{4, 0, 2, 3, 5, 1},{5, 4, 2, 3, 1, 0},{1, 5, 2, 3, 0, 4},
{5, 1, 3, 2, 4, 0},{1, 0, 3, 2, 5, 4},{0, 4, 3, 2, 1, 5},{4, 5, 3, 2, 0, 1},
{1, 3, 5, 0, 2, 4},{0, 3, 1, 4, 2, 5},{4, 3, 0, 5, 2, 1},{5, 3, 4, 1, 2, 0},
{3, 4, 5, 0, 1, 2},{3, 5, 1, 4, 0, 2},{3, 1, 0, 5, 4, 2},{3, 0, 4, 1, 5, 2},
};
int max(int x,int y)
{
if (x>=y) return x; else return y;
}
int min(int x,int y)
{
if (x>=y) return y; else return x;
}
int find(char* str)
{
for (int i=0;i<tj;i++)
if (strcmp(name[i],str)==0) return i;
strcpy(name[tj],str);
return tj++;
}
void init()
{
ans=30;
tj=0;
memset(name,0,sizeof(name));
memset(c,0,sizeof(c));
char w[30];
for (int i=0;i<n;i++)
{
for (int j=0;j<6;j++)
{
scanf("%s",w);
int id=find(w);
s[i][j]=id;
}
}
}
void work()
{
int v[30],sum=0;
for (int i=0;i<6;i++)
{
memset(v,0,sizeof(v));
int t=0;
for (int j=0;j<n;j++)
{
v[s[j][kn[c[j]][i]]]++;
t=max(t,v[s[j][kn[c[j]][i]]]);
}
sum+=n-t;
}
ans=min(sum,ans);
}
void dfs(int d)
{
if (d>=n)
{
work();
return;
}
for (c[d]=0;c[d]<24;c[d]++)
dfs(d+1);
}
int main()
{
cin>>n;
while (n!=0)
{
init();
dfs(1);
cout<<ans<<endl;
cin>>n;
}
return 0;
}