Description
某市的M公园中有一个近乎圆形的湖,有100个主要景点分布在湖边,为了方便游客,公园在一些景点之间开设了直通的摩托飞艇摆渡的项目一来减少游客在景点到景点之间所花的时间,二来也可以让游客体验一下惊险刺激的摩托飞艇。果然摩托飞艇摆渡项目大为成功,为了充分满足游客需要,摆渡线路越来越多。不料随着线路的增加,危险性也随之增加。如果两个摆渡线路之间有交叉(如上图),在这两个线路上的飞艇一旦发生碰撞,后果将不堪设想。
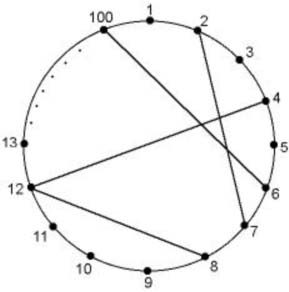
公园的管理层近日做出决定,本着安全第一的原则,在这个湖上取消一些线路,使剩下的任意两条线路在行驶阶段(即不考虑码头)不交叉。同时,考虑到经济效益,他们要求被取消的线路数最小,即保留尽量多的线路。他们希望你能够帮助他们算一算最多可以保留多少条线路。
Input
从文件line.in中读入数据,文件的第一行为N(1=
Output
将结果输出到文件line.out,文件只有一行,只有一个数,就是保留下来的线路的最多条数。
Sample Input
5
91 31
1 45
27 5
11 65
43 72
Sample Output
3
.
.
.
.
.
.
分析
本题的思路是使用floyd来计算最大保留边,f[i,j]表示i区间到j区间内最大保留边,方程:f[i,j]:=max(f[i,k]+f[k,j]+t,f[i,j]);(t为i,j之间是否存在边)
我们从i开始枚举,用i+l,也就是j(l是到下一个区间的距离)来更新各个点
因为i到j区间不可能只有这两个点,故用k来枚举i~j的各个点
最后在数组内找出最大保留边,并输出即可
.
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main()
{
int n,f[205][205];
memset(f,0,sizeof(f));
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
if (x>y) swap(x,y);
f[x][y]=f[x+100][y+100]=1;
}
int ans=0;
for (int l=2;l<=100;l++)
for (int i=1;i<=200-l-1;i++)
{
int a=i,b=i+l-1,t=0;
for (int k=a+1;k<=b-1;k++)
t=max(t,f[a][k]+f[k][b]);
f[a][b]+=t;
ans=max(ans,f[a][b]);
}
printf("%d",ans);
return 0;
}