（DP 雷格码）Gray code -- hdu -- 5375

http://acm.hdu.edu.cn/showproblem.php?pid=5375

 

Gray code

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 988    Accepted Submission(s): 551

Problem Description

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



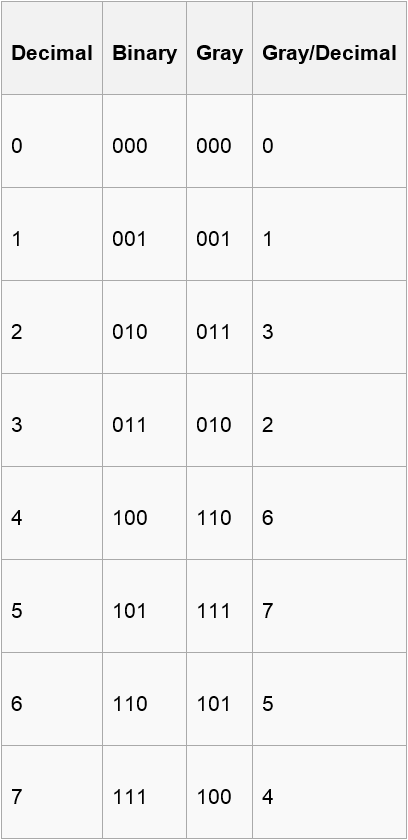
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

 

 

Input

The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

 

 

Output

For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most

 

 

Sample Input

2

00?0

1 2 4 8

????

1 2 4 8

 

 

Sample Output

Case #1: 12

Case #2: 15

 

雷格码：

从左边第二位起，将每位与左边一位解码后的值异或，

作为该位解码后的值（最左边一位依然不变）

 

 

DPor模拟

 

明白格雷码转二进制怎么转就好做，DP的话dp[i][j]代表i这个位置数字是j(0or1)的时候的最大值。
如果不是问号可能某些情况是不能到达的，不能到达的情况赋一个极小值就好了。

 

模拟的话就是一个类似于贪心的思路，其实就是找出一串问号两边是什么情况，一串问号我们可以全转化为1，但是邻接的非问号字符不一定是什么情况，如果一边一个0一边一个1的话就贪心进行取舍就好了

 

 

 

 

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;

const int N = 200005;
const int oo = 0x3f3f3f3f;

char s[N];
int dp[N][2], a[N];

int main()
{
    int T, iCase=1;

    scanf("%d", &T);

    while(T--)
    {
        int len, i;
        scanf("%s", s);

        len = strlen(s);

        for(i=0; i<len; i++)
          dp[i][0] = dp[i][1] = -oo;
        memset(a, 0, sizeof(a));

        for(i=0; i<len; i++)
            scanf("%d", &a[i]);

        if(s[0]=='1' || s[0]=='?')
            dp[0][1] = a[0];
        if(s[0]=='0' || s[0]=='?')
            dp[0][0] = 0;

        for(i=1; i<len; i++)
        {
            if(s[i]=='1' || s[i]=='?')
              dp[i][1] = max(dp[i-1][1], dp[i-1][0]+a[i]);
            if(s[i]=='0' || s[i]=='?')
              dp[i][0] = max(dp[i-1][0], dp[i-1][1]+a[i]);
        }

        printf("Case #%d: %d
", iCase++,  max(dp[len-1][0], dp[len-1][1]));
    }

    return 0;
}