题目描述
小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个m行n列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用0表示），可以用一个0-100的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度只和最大。现在，请你帮助小渊和小轩找到这样的两条路径。
输入输出格式
输入格式：
输入文件message.in的第一行有2个用空格隔开的整数m和n，表示班里有m行n列（1<=m,n<=50）。
接下来的m行是一个m*n的矩阵，矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度。每行的n个整数之间用空格隔开。
输出格式：
输出文件message.out共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
输入输出样例
说明
【限制】
30%的数据满足：1<=m,n<=10
100%的数据满足：1<=m,n<=50
NOIP 2008提高组第三题
这道题主要就是想说一说思路。
一个就是dp的思路。以前经常不知道怎么想，都是瞎猜状态。但其实应该从高维开始考虑，就最简单的把所有需要的变量都建一个维（一般来说最多也就4~5维）。同时还要考虑数据范围，可以计算出最多几维可以过。之后根据需要降维。
接下来是这道题。
我一开始是完全按照题目所说的，一个人从（1,1）出发，一个人从（n,m）开始。但不知道为什么答案是错的。这个我到现在也不太明白为什么，如果有知道的大佬可以在评论里解释一下，感激不尽~
总之后来就改成了两个人都是从（1,1）开始。接下来要处理的就是交叉点的问题。这里我刚开始也没想明白，以为题目中说一个人只能帮忙传一次，所以遇到两个人走到同一个位置就continue了。后来看了别人的题解才明白。这里放三张图：
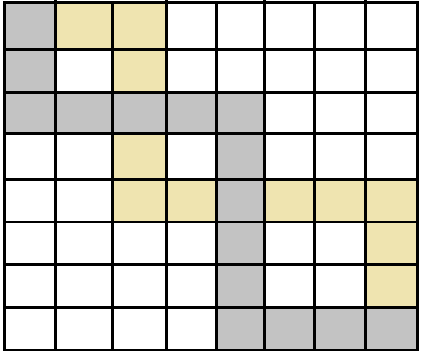假设这是两个人走过的一条有交叉点的路径
可以发现，这里把中间两人交叉的一段路径交换了过来。这对于结果是没有影响的。绿色的两块是交叉点。
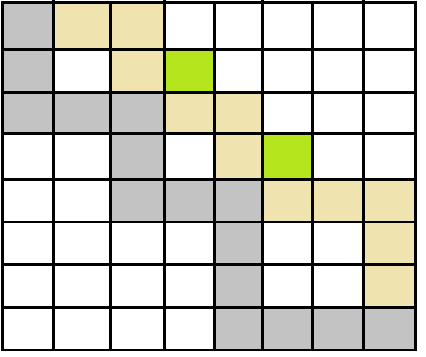我们把路径这么改，即把交叉点放到两个没有走过的块上。由于每个块都是0~100的正整数，所以多出来这两个块后结果一定比有交叉点时的大。因此图二的那种有交叉点的情况，虽然不允许发生，但即使发生了也不会是最大值。所以我们不用特别处理交叉点，只需要在交叉的时候剪掉一个重复的，避免其影响结果即可
（最后一步真的神来之笔。根本没有想到...）
1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 using namespace std; 8 int map[55][55]; 9 int f[55][55][55][55]; 10 int main() 11 { 12 int n,m; 13 scanf("%d%d",&n,&m); 14 for(int i=1;i<=n;i++) 15 for(int j=1;j<=m;j++) 16 scanf("%d",&map[i][j]); 17 for(int i=1;i<=n;i++) 18 for(int j=1;j<=m;j++) 19 for(int k=1;k<=n;k++) 20 for(int l=1;l<=m;l++) 21 { 22 f[i][j][k][l]=max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))+map[i][j]+map[k][l]; 23 if(i==k && j==l) f[i][j][k][l]-=map[i][j]; 24 } 25 printf("%d",f[n][m][n][m]); 26 return 0; 27 }