%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%汪神
P3806 【模板】点分治1
题目描述
给定一棵有n个点的树
询问树上距离为k的点对是否存在。
输入输出格式
输入格式:
n,m 接下来n-1条边a,b,c描述a到b有一条长度为c的路径
接下来m行每行询问一个K
输出格式:
对于每个K每行输出一个答案,存在输出“AYE”,否则输出”NAY”(不包含引号)
输入输出样例
说明
对于30%的数据n<=100
对于60%的数据n<=1000,m<=50
对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000
这道和上一道略有不同,是计算刚好等于k的点对是否存在,同时还是多组数据。我们只需要找一次,记录所有的点对距离,之后每输入一个k直接判断就好。
**本题重点**
可能会有算重的情况,如下:
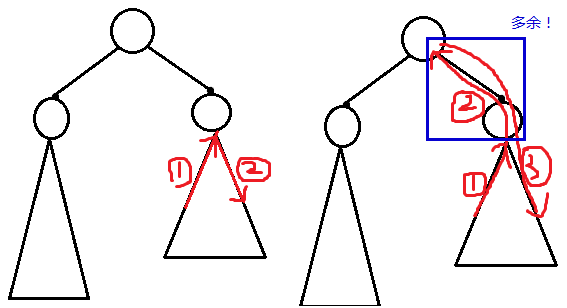
代码里巧妙地用ad来表示+1还是-1。这种表示方法要记住,以后应该还会用得到。

1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 #define MAXN 10010 8 using namespace std; 9 long long m,k,ans[20101010],ff[20010]; 10 int cnt,root,sn,tot; 11 int first[MAXN],to[20010],len[20010],next[20010],son[MAXN],deep[MAXN],vis[MAXN],f[MAXN],d[MAXN]; 12 void add(int x,int y,int z) //建立邻接表 13 { 14 to[++cnt]=y;len[cnt]=z; //to数组是当前边的下一条边的编号 15 next[cnt]=first[x]; //next数组记录当前起始点的前一条边的编号 16 first[x]=cnt; //first最终记录的是当前点作为起始点的最后一条边,之后从后往前遍历 17 } 18 void get_root(int x,int fa) //找重心 19 { 20 f[x]=0,son[x]=1; //f数组记录以x为根最大子树的大小 21 for(int i=first[x];i;i=next[i]) 22 if(to[i]!=fa && !vis[to[i]]) //不用考虑根节点以及没有访问过 23 { 24 get_root(to[i],x); 25 son[x]+=son[to[i]]; //计算x结点大小 26 f[x]=max(f[x],son[to[i]]); //找到最大子树 27 } 28 f[x]=max(f[x],sn-son[x]); 29 if(f[root]>f[x]) root=x; //更新当前根 30 } 31 void get_deep(int x,int fa) //求当前x为根节点的树的深度 32 { 33 d[++tot]=deep[x]; //每两个点之间的距离值都要记录 34 ff[tot]=x; 35 for(int i=first[x];i;i=next[i]) 36 if(to[i]!=fa && !vis[to[i]]) 37 { 38 deep[to[i]]=deep[x]+len[i]; 39 get_deep(to[i],x); 40 } 41 } 42 void calc(int x,int ad) 43 { 44 tot=0; 45 get_deep(x,0); 46 int i=1,j=tot,sum=0; 47 for(int i=1;i<tot;i++) //求个数 48 { 49 for(int j=i+1;j<=tot;j++) 50 { 51 if(ff[i]!=ff[j]) ans[d[i]+d[j]]+=ad; 52 } 53 } 54 55 } 56 void dfs(int x) 57 { 58 deep[x]=0; 59 vis[x]=1; 60 calc(x,1); 61 for(int i=first[x];i;i=next[i]) 62 { 63 if(!vis[to[i]]) //**// 64 { 65 calc(to[i],-1); 66 deep[to[i]]=len[i]; 67 sn=son[to[i]]; 68 root=0; 69 get_root(to[i],0); 70 dfs(root); 71 } 72 } 73 } 74 int main() 75 { 76 int n,x,y,z; 77 scanf("%d%lld",&n,&m); 78 memset(first,0,sizeof(first)); 79 memset(vis,0,sizeof(vis)); 80 cnt=0; 81 for(int i=1;i<n;i++) 82 { 83 scanf("%d%d%d",&x,&y,&z); 84 add(x,y,z); //无向图,建两次 85 add(y,x,z); 86 } 87 f[0]=0x7fffffff;sn=n; 88 root=0;get_root(1,0);dfs(root); 89 for(int i=1;i<=m;i++) 90 { 91 scanf("%lld",&k); 92 if(ans[k]>0) printf("AYE "); 93 else printf("NAY "); 94 } 95 return 0; 96 }
