注意:本文所有的排名均是从第0名开始。
康托展开:
已知一个$1—n$的排列$A={a_1,a_2,cdots,a_n}$,求它在所有排列中的字典序排名。
常用于将$n$的全排列映射到$n!$个自然数中。
求解这个问题的思路大概是下面这样的:
$(1)$ $A$的排名=字典序小于$A$的排列个数。所以只需要知道有多少个排列比$A$小就好了。
$(2)$ 我们按位考虑,第一位小于$a_1$的所有排列肯定比$A$小,这部分有$(a_{1}-1) imes (n-1)!$个。
$(3)$ 在第一个数等于$a_1$的所有排列中,第二位小于$a_2$的所有排列也肯定比$A$小。
那么这部分有$(a_{2}-1) imes (n-2)!$个对不对?
但是这个时候出现了一个问题:
如果$a_{1}<a_{2}$,那么第二位就不能再用$a_1$这个数了(因为是排列)。
所以应该有$(a_{2}-2) imes (n-2)!$个。
当然如果$a_{1}>a_{2}$就不需要额外$-1$了。
$(4)$ 现在我们把$(3)$的结论推广,
前$i-1$位与$A$相同且第$i$位小于$A$的排列,共有$(a_{i}-cnt_{i}-1) imes (n-i)!$个。
其中$cnt_i$表示前$i-1$个数${a_{1},a_{2},cdots ,a_{i-1}}$中小于$a_i$的个数。
显然所有这样的排列加起来就是比$A$小的排列总数(有序统计)。
$(5)$ 注意到$a_{i}-cnt_{i}-1$还等于后$n-i$个数${a_{i+1},a_{i+2},cdots ,a_{n}}$中小于$a_i$的个数(因为是排列……)。
所以我们就得到了康托展开公式:
$Rank_{A}=b_{n} imes (n-1)!+b_{n-1} imes (n-2)!+cdots +b_1 imes 0!$
其中$b_{i}$表示$a_i$在后$n-i$个数中排在第几个。
由于我们是从前往后处理,$b_i$也就相当于$a_i$在当前未出现的数中排在第几个。
代码:
inline int Cantor(){ int rank=0; for(int i=1;i<=N;i++){ int s=0; for(int j=i+1;j<=N;j++) s+=(A[j]<A[i]); rank+=s*jc[N-i]; } return rank; }
逆康托展开:
和上面相反,已知某排列的排名$x$,求这个排列。
解决思路基本没区别(说是相反也行):
假设我们现在要求$a_i$的值,首先可以得到$b_i=xdiv (n-i)!$。
那么也就是知道了$a_i$在当前未出现过的$a$中的排名。
但仅仅知道这个不能直接计算,所以我们还要记录一下前$i-1$位出现过的$a$。
然后$O(n)$枚举求出答案。
下面是一个例子:
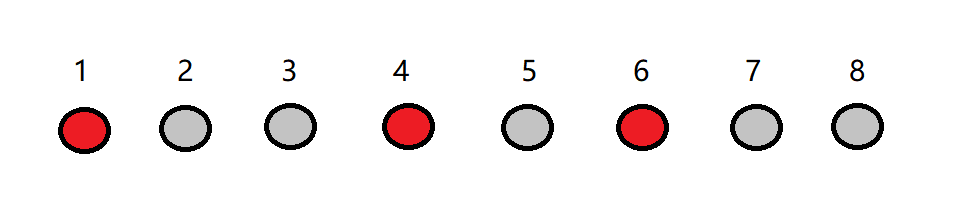
此时$n=8,i=4$,前$3$位出现了$1,4,6$。
假设$b_i=3$,那么$a_i$在未出现的数里排名第$3$。
由于排名是从$0$开始的,$a_i$就是灰色的第$4$个数$7$。
代码:
inline void inv_Cantor(int x){ memset(vis,0,sizeof(vis)); for(int i=1;i<=N;i++){ int tp=x/jc[N-i]; for(int j=1;j<=N;j++){ if(vis[j]) continue; if(tp==0){ vis[j]=1,A[i]=j; break; } tp--; } x=x%jc[N-i]; } return; }
模板题目:loj10027
(这题的排名是从1开始的)
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; #define MAXN 10 #define MAXM 1000005 #define INF 0x7fffffff #define ll long long inline int read(){ int x=0,f=1; char c=getchar(); for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; } int N=8,dis[MAXM],com[MAXM]; int jc[MAXN],A[MAXN],last[MAXM]; bool vis[MAXM],vvis[MAXN]; inline int Cantor(){ int rank=0; for(int i=1;i<=N;i++){ int s=0; for(int j=i+1;j<=N;j++) s+=(A[j]<A[i]); rank+=s*jc[N-i]; } return rank+1; } inline void inv_Cantor(int x){ x-=1; memset(vvis,0,sizeof(vvis)); for(int i=1;i<=N;i++){ int tp=x/jc[N-i]; for(int j=1;j<=N;j++){ if(vvis[j]) continue; if(tp==0){ vvis[j]=1,A[i]=j; break; } tp--; } x=x%jc[N-i]; } return; } inline int get1(int x){ inv_Cantor(x); swap(A[1],A[8]); swap(A[2],A[7]); swap(A[3],A[6]); swap(A[4],A[5]); return Cantor(); } inline int get2(int x){ inv_Cantor(x); swap(A[1],A[4]); swap(A[2],A[4]); swap(A[3],A[4]); swap(A[5],A[8]); swap(A[5],A[6]); swap(A[6],A[7]); return Cantor(); } inline int get3(int x){ inv_Cantor(x); swap(A[3],A[7]); swap(A[2],A[3]); swap(A[6],A[7]); return Cantor(); } inline void init(){ jc[0]=1; for(int i=1;i<=N;i++) jc[i]=jc[i-1]*i; return; } inline void print(int u){ if(u==1) return; print(com[u]); if(last[u]==1) printf("A"); if(last[u]==2) printf("B"); if(last[u]==3) printf("C"); } void BFS(){ int end=Cantor(); queue<int> q; q.push(1); dis[1]=0,vis[1]=1; while(!q.empty()){ int u=q.front(); q.pop(); if(u==end){ printf("%d ",dis[u]); print(u); printf(" "); break; } int t1=get1(u),t2=get2(u),t3=get3(u); if(!vis[t1]){ dis[t1]=dis[u]+1,vis[t1]=1; last[t1]=1,com[t1]=u; q.push(t1); } if(!vis[t2]){ dis[t2]=dis[u]+1,vis[t2]=1; last[t2]=2,com[t2]=u; q.push(t2); } if(!vis[t3]){ dis[t3]=dis[u]+1,vis[t3]=1; last[t3]=3,com[t3]=u; q.push(t3); } } return; } int main(){ for(int i=1;i<=N;i++) A[i]=read(); init(); BFS(); return 0; }