【UVA】P1510 Neon Sign (3000ms,0MB)
JungHeum recently opened a restaurant called ‘Triangle’ and has ordered the following neon sign for his
restaurant. The neon sign has N corners positioned on the circumference of a circle, and N ∗(N −1)/2
luminous tubes that connect the corners. There are only two colors for luminous tubes, red and blue.
JungHeum wants the sign to show only one shape of a triangle at a time, whose luminous tubes
colors are same, continuously. Hence, he wants to know the number of uni-color triangles.
For example, the following neon sign has only two uni-color triangles (1, 3, 5) and (2, 3, 4).
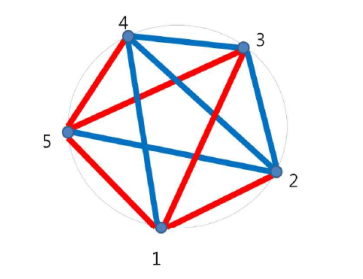
Given the number of corners of the neon sign and the colors of the luminous tubes in the sign, write
a program that finds the number of uni-color triangles.
Input
Your program is to read from standard input. The input consists of T test cases. The number of test
cases T is given in the first line of the input. Each test case starts with an integer N (3 ≤ N ≤ 1,000),
which represents the number of corners of the neon sign. In the following N − 1 lines, the information
about the color of the luminous tubes are given. For the i-th line of these lines, the color information
of the luminous tubes that connect corner i to corners from corner i+1 to N are given. Note that the
color red is represented as ‘1’ and the color blue is represented as ‘0’.
Output
Your program is to write to standard output. Print exactly one line for each test case. The line should
contain the number of uni-color triangles.
The following shows sample input and output for two test cases.
Sample Input
2
5
1 1 0 1
0 0 0
0 1
1
5
1 1 1 1
0 0 1
0 1
1
Sample Output
2
4
题解:<正难则反>
N个点的完全图,可以算出总三角形个数sum = C(N,3)
然后用三重循环穷举三个点构成三角形,当发现有2条边颜色不同时,sum -- 即可
因为时间限制是3s,所以不虚。
#include<bits/stdc++.h>
using namespace std;
int T,n,mp[1005][1005],sum;
int main()
{
scanf("%d",&T);
for (int i = 1 ; i <= T ; i ++)
{
scanf("%d",&n);
for (int j = 1 ; j < n ; j ++)
for (int k = j + 1 ; k <= n ; k ++)
{
int x;
scanf("%d",&x);
mp[j][k] = x;
}
sum = n*(n-1)*(n-2)/6;
for (int i = 1 ; i <= n - 2 ; i ++)
for (int j = i + 1 ; j <= n - 1 ; j ++)
for (int k = j + 1 ; k <= n ; k ++)
if (mp[i][j] != mp[i][k] || mp[i][j] != mp[j][k] || mp[i][k] != mp[j][k]) sum --;
printf("%d
",sum);
}
return 0;
}