Arpa is researching the Mexican wave.
There are n spectators in the stadium, labeled from 1 to n. They start the Mexican wave at time 0.
- At time 1, the first spectator stands.
- At time 2, the second spectator stands.
- ...
- At time k, the k-th spectator stands.
- At time k + 1, the (k + 1)-th spectator stands and the first spectator sits.
- At time k + 2, the (k + 2)-th spectator stands and the second spectator sits.
- ...
- At time n, the n-th spectator stands and the (n - k)-th spectator sits.
- At time n + 1, the (n + 1 - k)-th spectator sits.
- ...
- At time n + k, the n-th spectator sits.
Arpa wants to know how many spectators are standing at time t.
The first line contains three integers n, k, t (1 ≤ n ≤ 109, 1 ≤ k ≤ n, 1 ≤ t < n + k).
Print single integer: how many spectators are standing at time t.
10 5 3
3
10 5 7
5
10 5 12
3
In the following a sitting spectator is represented as -, a standing spectator is represented as ^.
- At t = 0 ----------
 number of standing spectators = 0.
number of standing spectators = 0. - At t = 1 ^---------
 number of standing spectators = 1.
number of standing spectators = 1. - At t = 2 ^^--------
 number of standing spectators = 2.
number of standing spectators = 2. - At t = 3 ^^^-------
 number of standing spectators = 3.
number of standing spectators = 3. - At t = 4 ^^^^------
 number of standing spectators = 4.
number of standing spectators = 4. - At t = 5 ^^^^^-----
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 6 -^^^^^----
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 7 --^^^^^---
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 8 ---^^^^^--
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 9 ----^^^^^-
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 10 -----^^^^^
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 11 ------^^^^
 number of standing spectators = 4.
number of standing spectators = 4. - At t = 12 -------^^^
 number of standing spectators = 3.
number of standing spectators = 3. - At t = 13 --------^^
 number of standing spectators = 2.
number of standing spectators = 2. - At t = 14 ---------^
 number of standing spectators = 1.
number of standing spectators = 1. - At t = 15 ----------
 number of standing spectators = 0.
number of standing spectators = 0.
题目大意:第T个时刻第T-k个人坐下,问T时刻站着多少人。
代码:
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
#define LL long long
inline int read(){
int x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
const int INF=9999999;
const int MAXN=100000;
int N,K,T;
int main(){
N=read(),K=read(),T=read();
if(T>=K&&T<=N) printf("%d
",K);
else if(T>N) printf("%d
",K-(T-N));
else printf("%d
",T);
return 0;
}
Arpa is taking a geometry exam. Here is the last problem of the exam.
You are given three points a, b, c.
Find a point and an angle such that if we rotate the page around the point by the angle, the new position of a is the same as the old position of b, and the new position of b is the same as the old position of c.
Arpa is doubting if the problem has a solution or not (i.e. if there exists a point and an angle satisfying the condition). Help Arpa determine if the question has a solution or not.
The only line contains six integers ax, ay, bx, by, cx, cy (|ax|, |ay|, |bx|, |by|, |cx|, |cy| ≤ 109). It's guaranteed that the points are distinct.
Print "Yes" if the problem has a solution, "No" otherwise.
You can print each letter in any case (upper or lower).
0 1 1 1 1 0
Yes
1 1 0 0 1000 1000
No
In the first sample test, rotate the page around (0.5, 0.5) by  .
.
In the second sample test, you can't find any solution.
题目大意:给定三个点A,B,C,问是否能通过选定一个点为中心点旋转a°使得A在B位置,B在C位置。
试题分析:只需要判断AB==BC,以及ABC是否在一条直线上就AC了……
“你距离正解,只有一个long long的距离”
代码:
#include<iostream>
#include<cmath>
using namespace std;
#define LL long long
inline long long read(){
long long x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
long long Ax,Ay,Bx,By,Cx,Cy;
double dist(long long x2,long long y2,long long x1,long long y1){
double xp=(x2-x1);double yp=(y2-y1);
return (double) sqrt(xp*xp+yp*yp);
}
int main(){
Ax=read(),Ay=read(),Bx=read(),By=read(),Cx=read(),Cy=read();
//if(Ax==Cx&&Ay==Cy){puts("Yes");}
if(dist(Ax,Ay,Bx,By)==dist(Bx,By,Cx,Cy)&&(Ay-Cy)*(Ax-Bx)!=(Ay-By)*(Ax-Cx)) {
puts("Yes");
}
else puts("No");
return 0;
}
You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.
We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 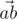 and
and  is acute (i.e. strictly less than
is acute (i.e. strictly less than 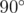 ). Otherwise, the point is called good.
). Otherwise, the point is called good.
The angle between vectors 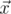 and
and 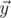 in 5-dimensional space is defined as
in 5-dimensional space is defined as 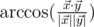 , where
, where 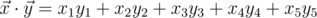 is the scalar product and
is the scalar product and  is length of
is length of  .
.
Given the list of points, print the indices of the good points in ascending order.
The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.
The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — the coordinates of the i-th point. All points are distinct.
First, print a single integer k — the number of good points.
Then, print k integers, each on their own line — the indices of the good points in ascending order.
6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1
1
3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0
0
In the first sample, the first point forms exactly a 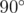 angle with all other pairs of points, so it is good.
angle with all other pairs of points, so it is good.
In the second sample, along the cd plane, we can see the points look as follows:
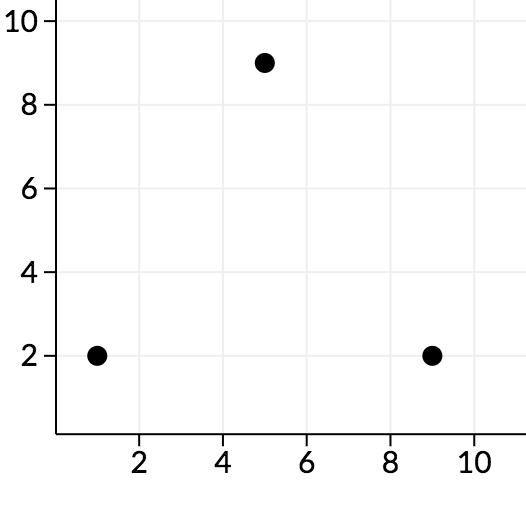
We can see that all angles here are acute, so no points are good.
题目大意:一个五维空间,当一个点与其它两个点形成90°时那么这个点是坏的,求有多少坏点。
试题分析:不知道怎么求向量的坐标……
acos(0)=90,所以说只需要上面那项等于0就统计,暴力好像可以过……