一、概念
高精
解题的过程中往往会遇到一些特殊的情况
求出超过20位的整数GCD或者是求和求积求差balbala……
C++中最大范围整数类型long long int范围1.84 * 10 19
超出这个范围就要用到高精计算
基本思想
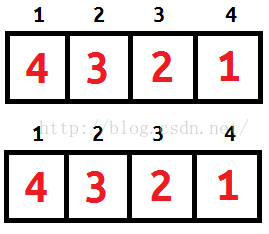
考虑在数组的每一个存储单元存储整数的每一位
比如:1234 把它变成1 2 3 4 考虑做一些小学生的工作
将1 2 3 4和5 6 7 8进行按位相加(减乘除)
得出的数依然在数组中存储 这样就可以实现对一个很大很大数字进行计算
适当优化
如果万恶的出题人给出两个几千位的数字要求求他们的积
暴力高精如果加上进位等常数很有可能T掉
这是就需要一个压位的思想 后面会进行解释
二、高精加
高精加是高精中比较简单的一类
模拟小学一年级第二学期加法内容即可
就像这样
需要注意的地方数组倒序储存
因为无法预知加法结果的长度 如果正着存储会导致向前(向左)进位可能没有空间进位
所以最方便的方法就是倒着储存
举个荔枝:
99 + 12
先读入 后处理
3 2 1
9 9
1 2 就是
1:9+2向左进位然后此位留下(9 + 2) % 10 = 1再算
2:9 + 1 再加上刚刚进的1 也就是9 + 1 + 1 继续进位 留下(9 + 1 + 1) % 10 = 1
这时候发现有效位数已经处理完 但是还有(9 + 1 + 1) / 10的余数x不为0 好的进一位
得到有效位数3: 留下1 % 10 = 1
得到答案111
上面的模拟中容易发现a位数的数+b位数的数可能是max(la,lb)或是max(la,lb)+1
所以实现的时候不妨设答案长度为max(la,lb) 如果有效位数处理完之后余数不为0
那么可以len++(因为我们是倒着储存的)再把余数存到ans[len]中
核心代码
1.初始化
使用字符串读入
如
scanf("%d",s);或scanf("%d",s+1); la = strlen(s);或 la = strlen(s+1);
利用
for(int i=1;i<=la;i++)
n1[la-i+1] = s[i]-'0';
//来实现对数字的倒序储存(习惯从 1 开始)
2.模拟加法
int add(int a[],int la,int b[],int lb,int c[]) //这里传进去的参数比较多 主要是方便运算 { int l=max(la,lb),x=0; //l为答案的长度,x是余数 for(int i=1;i<=l;i++){ c[i]=a[i]+b[i]+x;//竖式上下加上小下标 x=c[i]/10;//计算进位 c[i]%=10;//计算留下来的 } if(x!=0)c[++l]=x;//长度需要加1 return l;//返回答案的长度 便于输出答案 }
调用:
int len = add( a , la , b , lb , ans );
3.输出
for(int i = len ;i >= 1;i--) printf("%d" ,ans[i]);
三、压位
压位思想
还记得我们存储数字的方式?
举个栗子:1234 + 1234
这是之前的存储方式
实际上我们一个数组空间(int)是可以储存 2147483647 以下的数字 这样非常浪费 而且以上存储方式需要按位相加最后的计算次数是4
现在考虑这样的存储方式
这样相对上面的存储方式来说利用度较高
理解方式:考虑二进制 十进制 十六进制 的计算方式 满2进1 满10进1 满16进1
那么以上的存储方式请理解为100进制的计算 也就是满100进1
按照这样储存 按照(二)的规则计算 就是把1和2 3和4压到了同一个数组空间里 叫做压位
这样存储的数字计算次数就变成了2 很厉害的优化……
那我们为什么不这样呢
没错这是10000进制……
计算次数变成了1 其实仔细看一下就知道压位的思想就是把本来不用高精的计算尽量的扩大
来达到减少计算次数的目的
特殊的输出
在最后的输出答案部分 需要一些处理(下面假设写压P位的高精(也就是把P个数压到同一个数组空间里))
一句话概括:除最高位外,一切不足P位的数字输出时需要在前面补上0使得满足P位
比如压2位 2 + 99 为例 最后会用到两个数组空间(一个放1,一个放1…)但是这两个一代表的意义不同,
第二个可以原样输出因为这是最高位(即整个数的长度modP后得到的剩余部分 这一部分是独立于其他部分的 如果补上0 最后就是0101 是不对的),第一个就需要补上一个0来使得输出101而不是11
那么怎么实现呢 下面代码
#include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #define p 8//要压的位数 #define carry 100000000//相应的10的P次方 用于进位 //这样如果要改变压位的位数只要改这里就可以 using namespace std; const int Maxn=50001; char s1[Maxn],s2[Maxn]; int a[Maxn],b[Maxn],ans[Maxn]; int change(char s[],int n[])//压位的核心部分 { char temp[Maxn];//中间变量 记录每p位的数 int len=strlen(s+1),cur=0; while(len/p){//如果len大于等于p strncpy(temp,s+len-p+1,p);//从后面截出来p位数 n[++cur]=atoi(temp);//把temp搞成数字 len-=p;//继续下p位 } if(len){//如果最后len不是正好p的倍数 也就是还剩下点不够p位的 memset(temp,0,sizeof(temp)); strncpy(temp,s+1,len);//全截下来 n[++cur]=atoi(temp);//赋上 } return cur;//返回一个位数 } //这里就是(二)中的内容了 计算正常计算就行 int add(int a[],int b[],int c[],int l1,int l2) { int x=0,l3=max(l1,l2); for(int i=1;i<=l3;i++){ c[i]=a[i]+b[i]+x; x=c[i]/carry;//进位 c[i]%=carry; } while(x>0){c[++l3]=x%10;x/=10;} return l3;//返回答案的位数 } void print(int a[],int len) { printf("%d",a[len]);//处理高位 for(int i=len-1;i>=1;i--)printf("%0*d",p,a[i]);//输出p位 不足补0 printf(" "); } int main() { // freopen("t.in","r",stdin); // freopen("t.out","w",stdout); scanf("%s%s",s1+1,s2+1);//读入两个字符串 int la=change(s1,a);//将s1这个字符串转化为a这个整型数组 int lb=change(s2,b);//同上 int len=add(a,b,ans,la,lb); //计算长度为la的a数组和长度为lb的b数组最后把答案赋给ans数组 并顺便计算出ans的长度(便于输出) print(ans,len);//输出函数 }
四、高精减
思想
复杂度
代码
1.首先判断两数大小 如果是s1小于s2先输出“-”再交换最后计算
给出judge和swap
1 bool judge() 2 { 3 if(len1<len2){swap();return 1;} 4 if(len1>len2)return 0; 5 for(int i=len1;i>=1;i--) 6 if(b[i]>a[i]){swap();return 1;} 7 return 0; 8 }
void Swap() { memcpy(c,a,sizeof(a)); memset(a,0,sizeof(a)); memcpy(a,b,sizeof(b)); memset(b,0,sizeof(b)); memcpy(b,c,sizeof(c)); int len=len1;len1=len2;len2=len; }
2.默认s1减去s2
给出操作部分
int x=0; for(int i=1;i<=len1;i++) { temp[i]=a[i]-b[i]-x; x=(temp[i]<0)?1:0; temp[i]=(temp[i]<0)?temp[i]+10:temp[i]; } while(!temp[len1])len1--;
3.倒序输出答案即可
五、高精乘
高精度就是模拟小学生做四则运算的过程
高精度乘法只要注意一下答案和乘数的错位相加即可
思想
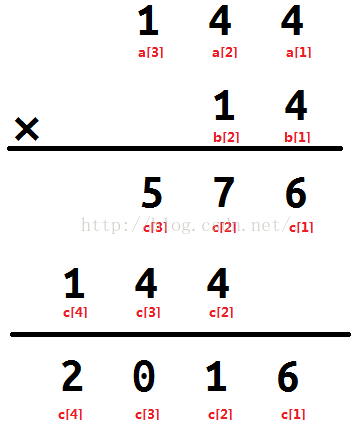
回到小学课堂……
基本的计算就是这样的
关于乘数和答案的错位相加问题 可以发现这样的规律:ans[i+j-1] + = a[i] * b[j];
关于为什么的问题可以请教小学老师……
特殊的地方
高精乘有一些特殊的地方
每次的的最外层for也就是在处理一个数的一位和另一个数的各个位的乘积向答案加的时候
如果最后余数不为0 需要向最后一位的下一位进行进位 具体看代码
压位
考虑压位的话把读入修改一下就可以
代码
for(int i = 1; i <= len1; i++) { x = 0; len = i + len2 - 1; for(int j = 1; j <= len2; j++) { temp[i + j - 1] += a[i] * b[j] + x; x = temp[i + j - 1] / 10; temp[i + j - 1] %= 10; } if(x>0) temp[++len]+=x; }
注意+=的细节
六、高精除
by YLCH P.S.除了板子一般不会有那个SB的出题人SB到出高精除,如果你真的在以后的OI之路上遇到了高精除。。。。。那么先在心里默默地骂while(1)遍出题人,然后不断地告诉自己,不要怕,高精除就是一直减。。。
高精除看起来很复杂
实际上就是一个 对位相减 的过程 因为是 对位相减 理论复杂度很小不会T
(这里介绍高精除高精,高精除低精相对简单,拿一个中间变量记一下就好了)
基本思想
还是考虑小学课堂的除法 下面看竖式
回想做除法竖式的情景 是不是先把27放到2835的最前面和28作比较看谁大谁小?
如果除数小于被除数的当前串那么就向上商答案商到被除数的当前串小于除数
在实际操作中可以用减法来模拟这个过程 每减一次就在对应除数尾部答案处加一来统计答案
还是举个例子:看上式,27在28处查看发现我比28小!那么进行一次减法操作使得2 8 - 2 7现在被除数变成1 3 5
再次查看时发现27比1要大了 此时不能再减 则将除数(2 7)的指针向后移 到了1 3的位置 发现还是小 指针再向后移动
到了3 5处 统计从头到指针的数字(即0 1 3 5)与除数(2 7)进行比较 发现可以操作 那么就进行减法操作
每次减完后都检查是否能继续减下去 然后ans[tail]++ 统计答案 tail即是尾指针
代码
#include <cstdio> #include <cstring> #include <iostream> using namespace std; #define tail head+len2-1//与head联动的tail 记录除数的尾部指针 #define Init len1=strlen(s1+1),len2=strlen(s2+1);//初始化 const int Maxn=10001; int len1,len2,cur=1; char s1[Maxn],s2[Maxn]; int a[Maxn],b[Maxn],c[Maxn],ans[Maxn]; bool compare(int head) { cur=1;while(a[cur]==0)cur++;//去除a前面的0 便于计算 if(tail-cur+1 > len2)return 1;//tail-cur+1即是当前串的长度 if(tail-cur+1 < len2)return 0; string str1="",str2="";//比大小 for(int i=cur;i<=tail;i++){ str1 += a[i]+48; str2 += b[i-head+1]+48; } if(str1>=str2)return 1;//使用重载过的String类比较 else return 0;//如果大于等于就减 小于则不能减 } int sub(int head) { for(int i=tail;i>=tail-len2+1;i--){//从后往前减 a[i]=a[i]-b[i-head+1];//减法 if(a[i]<0){//如果不够减借一位 a[i]+=10; a[i-1]--; } } ans[tail]++;//统计答案 } int main() { scanf("%s%s",s1+1,s2+1);Init//读入并处理出长度 for(int i=1;i<=len1;i++)a[i] = s1[i]-'0';//读入 for(int i=1;i<=len2;i++)b[i] = s2[i]-'0';//读入 for(int head=1;tail<=len1;head++){//查看该数放在哪一个位置 if( !compare(head) )continue;//如果a小于b 则继续下一层 即把b数往后挪一位 else while( compare(head) ) sub(head);//只要能减就一直减 直到a小于b 同时在tail处统计答案 } cur=1;while( ans[cur]==0 && cur!=len1 )cur++;//去除前面的0 for(int i=cur;i<=len1;i++)printf("%d",ans[i]);//输出 }
转自sSay学长CSDN blog:https://blog.csdn.net/sssSSSay/article/details/52100175
https://blog.csdn.net/sssSSSay/article/details/52101033
https://blog.csdn.net/ssssssay/article/details/52102173
https://blog.csdn.net/sssSSSay/article/details/52104396
https://blog.csdn.net/sssSSSay/article/details/52104610
https://blog.csdn.net/sssSSSay/article/details/52106713