平面向量的概念
有大小又有方向的量叫做向量
具有方向的线段叫做有向现段
有向线段包括三个要素:起点,方向,长度
向量大小,即向量长度,称为模,0叫做零向量
长度等于1的单位长度叫做单位向量
相等向量与共线向量
平行向量:方向相同或相反的非零向量
相等向量:长度相等且方向相同的向量
共线向量:平行向量也叫做共线向量
平面向量的运算
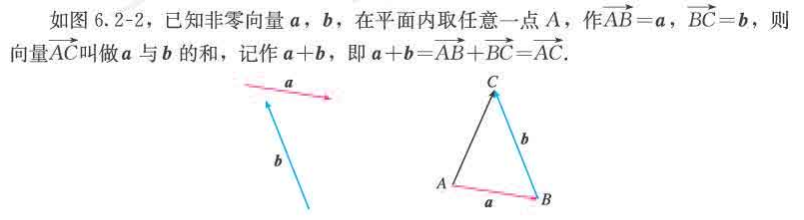
向量的加法运算
向量加法的三角形法则
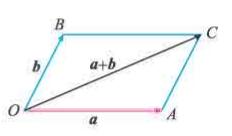
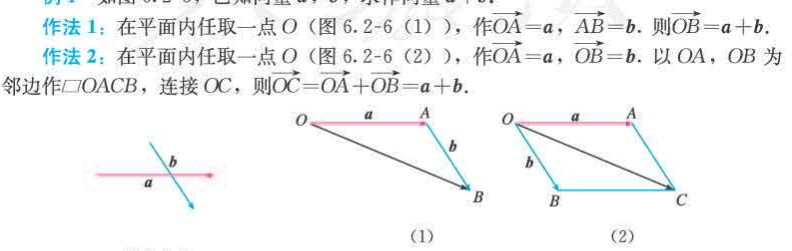
向量加法的平行四边形法则
对于零向量与任意向量,我们规定

向量的减法运算

零向量的反向量仍然是零向量
任意向量与其相反向量的和是零向量
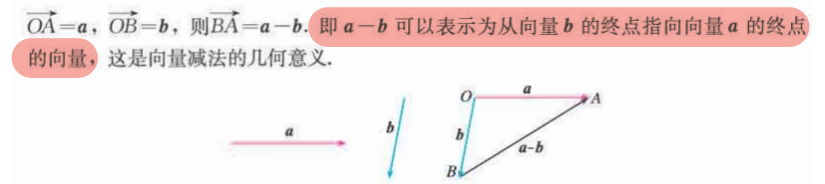
向量a加上b的相反向量,叫做a与b的差
求两个向量差的运算叫做向量的减法
向量减法的几何意义
向量的数乘运算


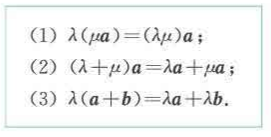

向量a与b共线的充要条件是,存在唯一一个实数α,使得b=αa
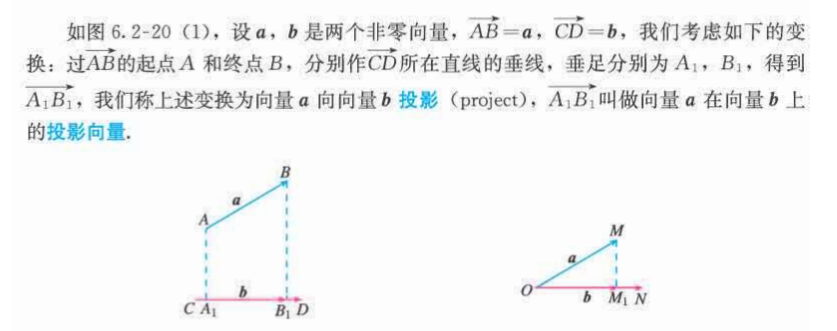
向量的数量积


零向量与任一向量的数量积为0



平面向量基本定理及其座标表示


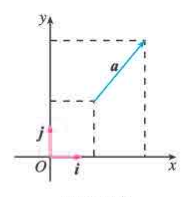
平面向量的正交分解及坐标表示
不共线的两个向量相互垂直是一种重要的情形,把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解

平面向量加、减运算的坐标表示

一个向量的坐标等于表示此向量的有向现段的终点坐标减去起点坐标
平面向量数乘运算的坐标表示

平面向量数量积的坐标表示



平面向量的应用

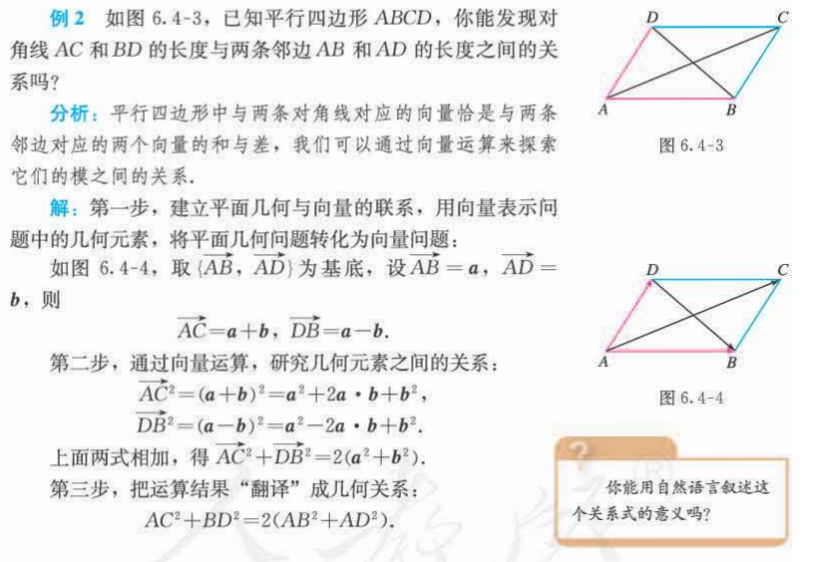
余弦定理、正弦定理


余弦定理

解三角形


正弦定理

向量法研究三角形性质
三角形的重心分每条中线为1:2的两条线段

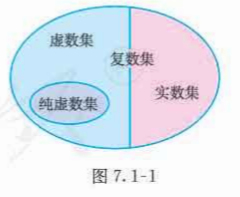
复数

虚数单根,复数集,实部,虚部,纯虚数,

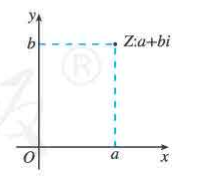
复数的几何意义
复平面,实轴,虚轴


共轭复数

复数的四则运算

满足交换律和结合律

复数的乘、除运算
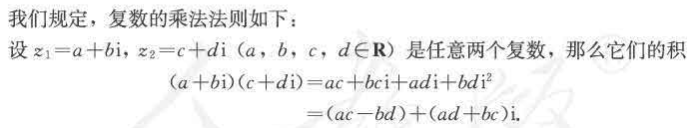

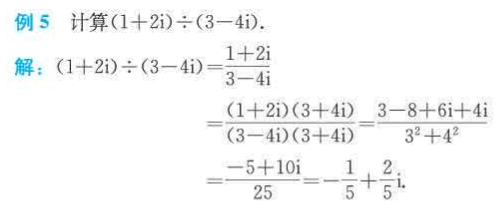

代数基本定理


复数的三角表示

三角形式,复数形式

复数乘、除运算的三角表示及其几何意义
复数的乘法


复数的除法

立体几何初步
基本立体图形,空间几何体
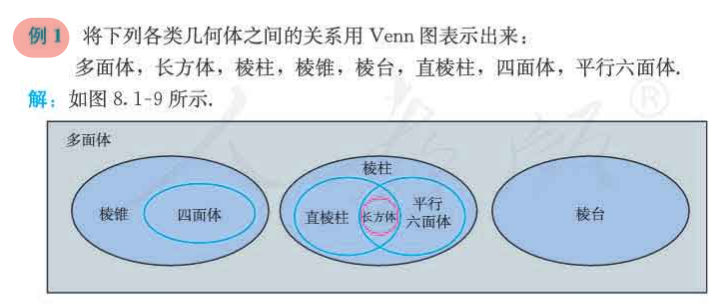
多面体,面,棱,顶点,旋转体,轴
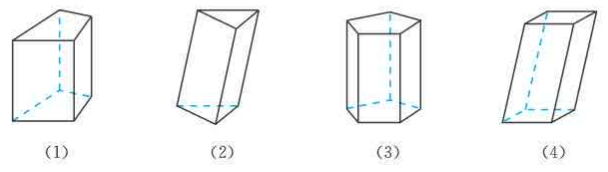
棱柱


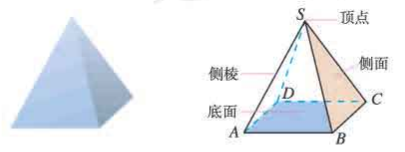
棱锥

正棱锥

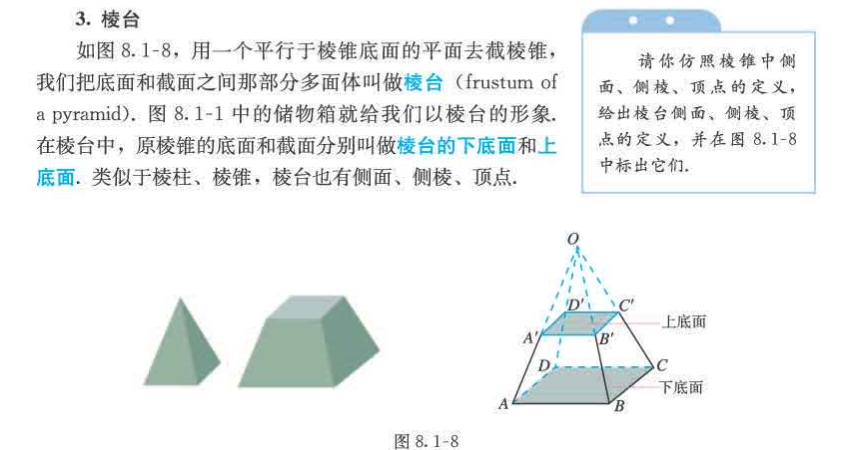
棱台
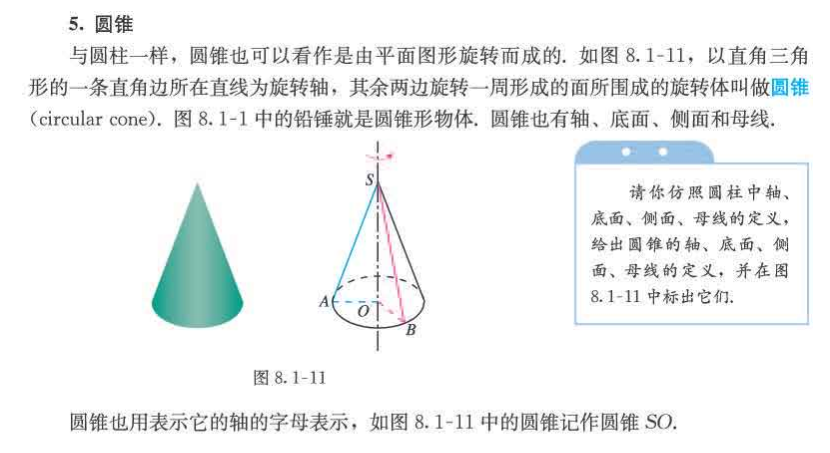
圆锥
圆台

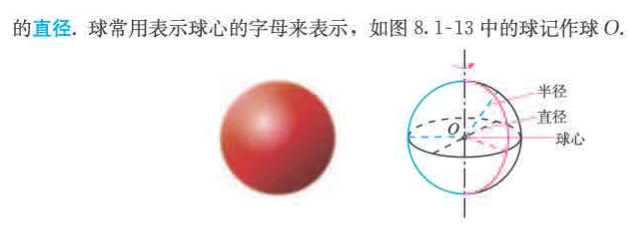
球

立体图形的直观图
斜二测画法
简单几何体的表面积与体积
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积


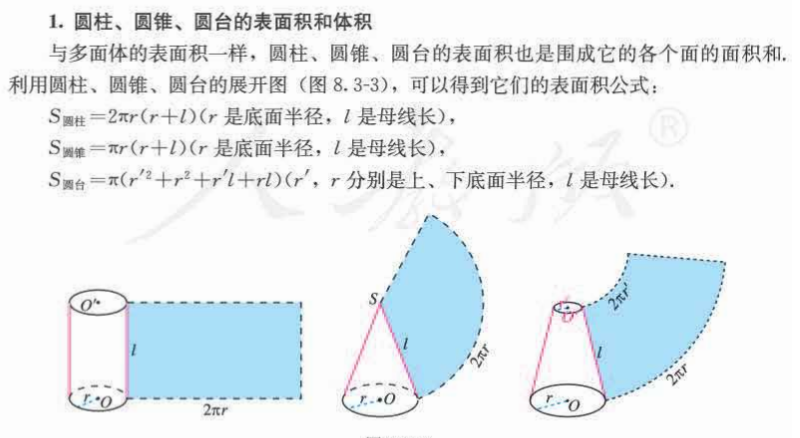
圆柱、圆锥、圆台、球的表面积和体积


空间点、直线、平面之间的位置关系


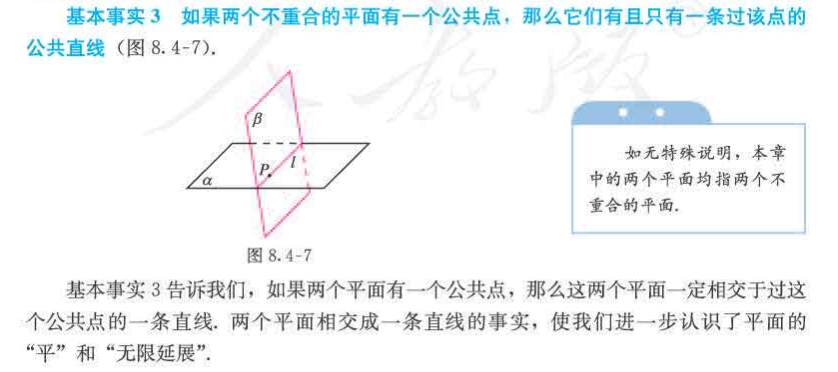
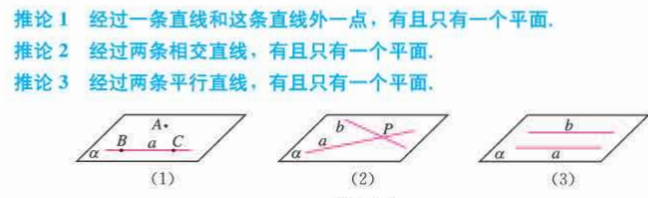
空间点、直线、平面之间的位置关系
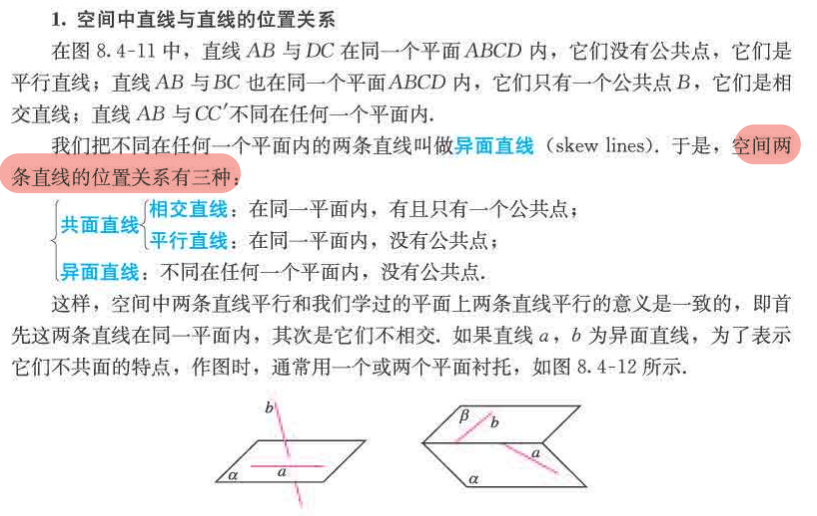
空间中直线与直线的位置关系
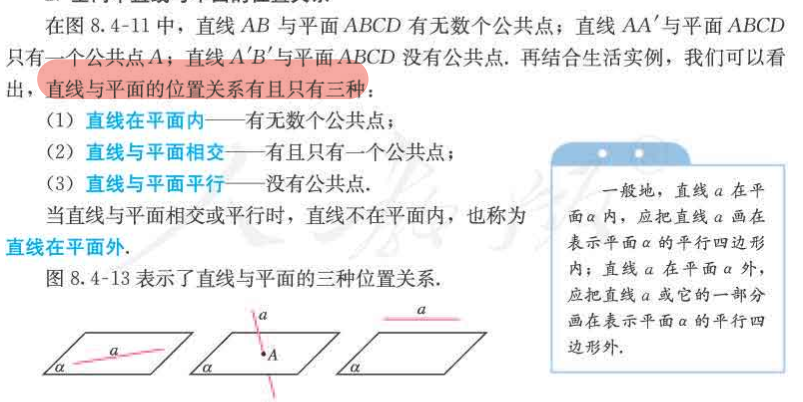
空间中直线与平面的位置关系
空间中平面与平面的位置关系

