

A 无穷处可能存在瑕点,此时p=1,q≤1,所以发散
B 无穷处可能存在瑕点,此时p=1,q=1,发散
C 无穷处可能存在瑕点,此时p=1,q=2,收敛
D 无穷处可能存在瑕点,此时p=1,q=1/2,发散

A 0处可能存在瑕点,x->0,等价于 1/x,所以发散

A 无穷处可能存在瑕点,p < 1,发散
B 无穷处可能存在瑕点,p = 1,q <= 1,发散
C 无穷处可能存在瑕点,p=1,q=1,发散
D 分部积分计算
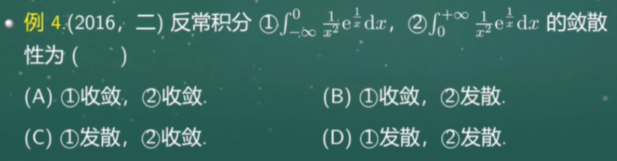
分部积分计算

A 伽马函数
B 凑微分直接计算
C 凑微分直接计算
D 凑微分直接计算
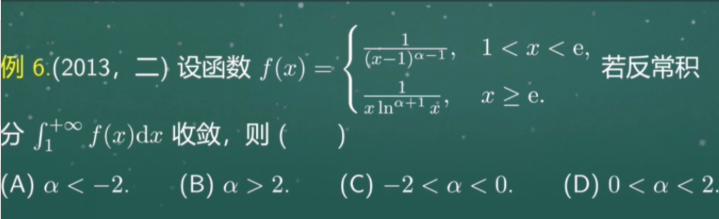
1处可能有瑕点,所以需要0 < α - 1 < 1,无穷处可能有瑕点,p = 1,需要 α + 1 > 1,取交集,D

0处可能有瑕点,0 < a < 1,无穷处可能有瑕点,a + b > 1

无穷处可能有瑕点,1 - p + 1 > 1,p < 1

第一个函数在∞处可能有瑕点,第二个函数在1处可能有瑕点,x的次方数是1,p-1 < 1收敛

二重积分中值定理

A 可以用积分判敛法,x比3^x趋向于∞速度慢
B n->∞,1 / n^3/2,收敛
C 分开两部分,前半部分,交错级数审敛法,后半部分 lnx < x,1 / lnn > 1/x,发散
D 把阶乘展开,1/n * 2/n * 3/n *... * n / n,收敛

第一个级数,n->∞,级数~1 / n^(α - 1/2),α - 1/2 > 1,第二个级数条件收敛, 0 < 2 - α <= 1

sin,有界震荡,合并以后,绝对收敛

分开看,前半部分,~ 1/n,后半部分,等价于 k / n,所以k=-1

an < 1/n,若 an = 1/2n,AC都不对,B 选项,若奇数项和偶数项通项不同,B不对