反常积分和变限求导积分都是由定积分推出来的
反常积分如果收敛,则可以用奇偶性
上下限为无穷,奇函数积分,不一定是对称的,因为无穷可以无限加,无法定量
但是取两个定值(-R, R),R趋向于∞,这个就不一样了,R是个定值,积分就是0了
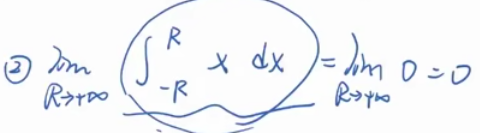

第二条,假设f(x)=x,这个极限存在且为0,但这个反常积分发散
第三条,这两个函数之和为0,如x + (-x),积分值为0,反常积分收敛
第四条,反常积分发散的定义
反常积分和变限求导积分都是由定积分推出来的
反常积分如果收敛,则可以用奇偶性
上下限为无穷,奇函数积分,不一定是对称的,因为无穷可以无限加,无法定量
但是取两个定值(-R, R),R趋向于∞,这个就不一样了,R是个定值,积分就是0了
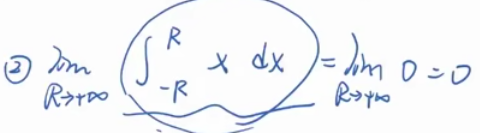

第二条,假设f(x)=x,这个极限存在且为0,但这个反常积分发散
第三条,这两个函数之和为0,如x + (-x),积分值为0,反常积分收敛
第四条,反常积分发散的定义