八大排序之选择类排序

直接插入排序

• 在有序数组中插入一个元素，可以作为一种排序方法的基础
• 只有一个元素的数组是一个有序数组，对n个元素的数组，可以从第一个元素所构成的单元数组开始，不断实施插入操作
• 插入第二个元素，得到2个元素的有序数组。插入第三个元素，得到3个元素的有序数组
• 如此反复，得到n个元素的有序数组

示例

对序列：6，5，8，4，3，1 进行直接插入排序

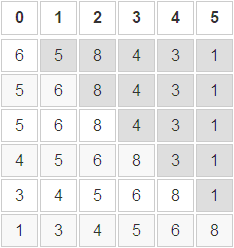
• 图中灰色部分代表待排序列
• 图中透明部分代表已排序列

// C++ program for insertion sort  
#include <bits/stdc++.h> 
using namespace std; 
  
/* Function to sort an array using insertion sort*/
void insertionSort(int arr[], int n)  
{  
    int i, key, j;  
    for (i = 1; i < n; i++) 
    {  
        key = arr[i];  
        j = i - 1;  
  
        /* Move elements of arr[0..i-1], that are  
        greater than key, to one position ahead  
        of their current position */
        while (j >= 0 && arr[j] > key) 
        {  
            arr[j + 1] = arr[j];  
            j = j - 1;  
        }  
        arr[j + 1] = key;  
    }  
}  
  
// A utility function to print an array of size n  
void printArray(int arr[], int n)  
{  
    int i;  
    for (i = 0; i < n; i++)  
        cout << arr[i] << " ";  
    cout << endl; 
}  
  
/* Driver code */
int main()  
{  
    int arr[] = { 12, 11, 13, 5, 6 };  
    int n = sizeof(arr) / sizeof(arr[0]);  
  
    insertionSort(arr, n);  
    printArray(arr, n);  
  
    return 0;  
}  
  
// This is code is contributed by rathbhupendra 

记法：

• 开辟一个临时变量，记录无序序列第一个元素
• 与有序序列的元素比较大小，从后往前
• 如果临时变量小于当前比较元素，当前比较元素后移一位
• 否则，临时变量占用当前比较位

时间复杂度分析

由直接插入排序代码，选取最内层

a[j + 1] = a[j];

作为基本操作语句

1. 考虑最坏的情况，即整个序列是逆序的，O(n^2)
2. 考虑最好的情况，即整个序列是有序的，O(n)

综上所述，本算法的平均时间复杂度O(n^2)

空间复杂度分析

• 算法所需的辅助存储空间不随待排序列规模的变化而变化，是个常量，O(1)

折半插入排序

• 与直接插入排序思想类似，区别是查找插入位置的方法不同，折半插入排序是采用折半查找法查找插入位置的
• 将待排序的记录R[i]，通过折半查找的方式在有序序列中查找插入位置

示例

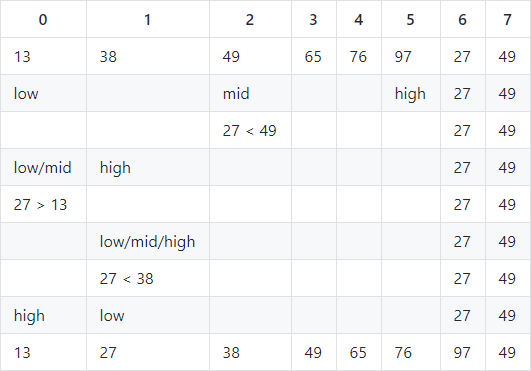
对序列：13，38，49，65，76，97，27，49进行一趟折半插入排序。

前6个元素已经排好序列，查找27的插入位置

1. mid = (0 + 5)/2 = 2，当前位置，27 < 49，27的插入位置在49的低半区
2. h = mid - 1，mid = (0 + 1)/2 = 0，当前位置，27 > 13，27插入位置在13的高半区
3. low = mid + 1，mid = (1 + 1)/2 = 1，27 < 38，27的插入位置在38低半区
4. high = m - 1 = 0，high < low，折半查找结束，27的插入位置在high之后，插入位置后面的元素后移

// C program for implementation of binary insertion sort 
#include <stdio.h> 

// A binary search based function to find the position 
// where item should be inserted in a[low..high] 
int binarySearch(int a[], int item, int low, int high) 
{ 
    if (high <= low) 
        return (item > a[low])? (low + 1): low; 

    int mid = (low + high)/2; 

    if(item == a[mid]) 
        return mid+1; 

    if(item > a[mid]) 
        return binarySearch(a, item, mid+1, high); 
    return binarySearch(a, item, low, mid-1); 
} 

// Function to sort an array a[] of size 'n' 
void insertionSort(int a[], int n) 
{ 
    int i, loc, j, k, selected; 

    for (i = 1; i < n; ++i) 
    { 
        j = i - 1; 
        selected = a[i]; 

        // find location where selected sould be inseretd 
        loc = binarySearch(a, selected, 0, j); 

        // Move all elements after location to create space 
        while (j >= loc) 
        { 
            a[j+1] = a[j]; 
            j--; 
        } 
        a[j+1] = selected; 
    } 
} 

// Driver program to test above function 
int main() 
{ 
    int a[] = {37, 23, 0, 17, 12, 72, 31, 
            46, 100, 88, 54}; 
    int n = sizeof(a)/sizeof(a[0]), i; 

    insertionSort(a, n); 

    printf("Sorted array: 
"); 
    for (i = 0; i < n; i++) 
        printf("%d ",a[i]); 

    return 0; 
} 

记法

• 开一个遍历，开辟一个临时变量，记录每次遍历的第一个的元素
• 临时变量与有序序列中间元素比较，小于则去底半区查找，大于则去高半区查找
• 若找到相同元素，则记录当前位置的后移一位
• 若找不到相同元素，小于low记录low的位置，大于low记录low的位置+1
• 最后交换相应位置（后移并插入的一个过程）

时间复杂度分析

• 折半插入排序适合关键字数较多的场景，与直接插入排序相比，折半插入排序在查找插入位置上面所花的时间大大减少
• 折半插入排序在关键字移动次数上面和直接插入排序是一样的，所以时间复杂度和直接插入排序还是一样的
• 可知折半插入排序的时间复杂度最好情况为O(nlog2n)，最差情况为O(n^2)，平均情况为O(n^2)

空间复杂度分析

同直接插入排序，O(1)

希尔排序(缩小增量排序)

• 将待排序列分成几个子序列，分别对这几个子序列进行直接插入排序

• 如果增量是1，那么就是直接插入排序

该方法实质上是一种分组插入方法

• 比较相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换

算法思想

• 先将要排序的一组数按某个增量d分成若干组，每组中记录的下标相差d

• 对每组中全部元素进行排序，然后再用一个较小的增量对它进行，在每组中再进行排序

• 当增量减到1时，整个要排序的数被分成一组，排序完成

示例

• 原始序列：49 38 65 97 76 13 27 45 55 04

• 分割线指向的元素做直接插入排序

// C++ implementation of Shell Sort
#include <iostream>
using namespace std;

/* function to sort arr using shellSort */
int shellSort(int arr[], int n)
{
    // Start with a big gap, then reduce the gap
    for (int gap = n/2; gap > 0; gap /= 2)
    {
        // Do a gapped insertion sort for this gap size.
        // The first gap elements a[0..gap-1] are already in gapped order
        // keep adding one more element until the entire array is
        // gap sorted
        for (int i = gap; i < n; i += 1)
        {
            // add a[i] to the elements that have been gap sorted
            // save a[i] in temp and make a hole at position i
            int temp = arr[i];

            // shift earlier gap-sorted elements up until the correct
            // location for a[i] is found
            int j;            
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
                arr[j] = arr[j - gap];
            
            // put temp (the original a[i]) in its correct location
            arr[j] = temp;
        }
    }
    return 0;
}

void printArray(int arr[], int n)
{
    for (int i=0; i<n; i++)
        cout << arr[i] << " ";
}

int main()
{
    int arr[] = {12, 34, 54, 2, 3}, i;
    int n = sizeof(arr)/sizeof(arr[0]);

    cout << "Array before sorting: ";
    printArray(arr, n);

    shellSort(arr, n);

    cout << " Array after sorting: ";
    printArray(arr, n);

    return 0;
}

希尔排序不稳定

• 增量序列的最后一个值一定取1

• 增量序列中的值尽量没有除1之外的公因子

时间复杂度

• 时间与步长选取有关，但目前没有对应解析表达式

空间复杂度O(1)