句型分析
- 句型分析是一个识别输入符号串是否为语法上正确的程序的过程
- 在语言的编译实现中，把完成句型分析的程序称为分析程序或识别程序，分析算法又称识别算法
该书介绍的都是从左到右的分析算法，从左到右地识别输入符号串
两大类分析算法
- 自顶向下，从文法开始符号出发，反复使用各种产生式，寻找"匹配"于输入符号串的推导 （正着推）
- 自底向上，从输入符号串开始，逐步进行"归约"，直至归约到文法的开始符号 （反着推）
- 从构造语法树的角度看，自顶向下，从树根开始构造；自底向上，从末端结点开始构造
自顶向下的分析方法
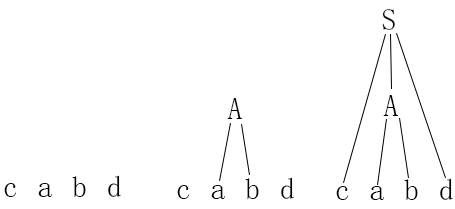
例题2.9 考虑文法G[S]
- S→sAd
- A→ab
- A→a
S=>cAd=>cabd
自底向上的分析方法
例题2.9中的文法来为输入符号 cabd 构造语法树
句型分析的有关问题
在自顶向下分析方法中，回溯
- 从各种可能的选择中随机挑选一种，并希望它是正确的
- 如果它是错误的，必须退回去，再试另外的选择
在自底向上分析方法中，句柄
- 需要精确定义"可归约串"，称为句柄
- 令G是一个文法，S是文法的开始符号，αβδ是文法G的一个句型
- 若有S
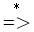αAδ 且 A
β，则称β是句型αβδ相对于非终结符号A的短语 
- 如果有 A=>β，则称β是句型αβδ相对于规则 A→β 的直接短语（简单短语）
-
一个右句型的直接短语，称为该句型的句柄，句柄的概念只适用于右句型
-
若所考虑的文法是无二义的，每个右句型有唯一的最右推导，句柄是唯一的；对于二义文法，右句型可能有 多个句柄
- 对于无二义文法，一个右句型的唯一句柄是其所有直接短语中最左边的那一个，该句型的最左直接短语即是它的句柄
举例
考虑例2.8 中的无二义文法G[E]的一个句型 i*i + i，将句型写作 i1 * i2 + i3 ，因为有 E 
F * i2 + i3，且 F => i1，则称 i1 是句型 i1 * i2 + i3 的相对于非终结符号F的短语，也是相对于规则 F→i 的直接短语
有关文法应用的一些说明
有关文法的实用限制
在实际应用中，应限制文法不得含有 有害规则 和 多余规则
- 有害规则，形为U→U的产生式，会引起文法的二义性
- 多余规则，文法中那些连一个句子的推导都用不到的规则，以两种形式出现
- 第一种是文法中某些非终结符不在任何规则的右部出现，任何句子的推导中都不可能用到他
- 第二种是文法中的非终结符号，不能够从它推导出终结符来
例题 2.10 有文法 G[S]：
- S→Be
- B→Ce
- B→Af
- A→Ae
- A→e
- C→Cf
- D→f
对文法G=（VN,VT,S,P）来说，为了保证其非终结符A在句子推导中出现，必须满足以下两个条件
- A必须在某句型中出现，有 S
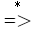αAβ，其中α、β∈（VN ∪ VT）* - 必须能够从A推出终结符号串t来，即 A
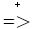t，其中∈V*T
在该例中，
- 非终结符D不在任何规则右部，这种非终结符称为不可到达
- 在文法中，不能够推导出终结符号串来，这种非终结符称为不可终止
上下文无关文法的ε规则
上下文中某些规则可具有形式 A→ε，其中A∈VN，这种称为ε规则
定理2.1
- 若L是由文法G=（VN，VT，P，S）产生的语言，P中的每一个产生式的形式均为A→α，A∈VN，α∈（VN ∪ VT）*
- L能由这样的一种文法产生，每一个产生式或者为A→β形式，其中A为一个非终结符，即 A∈VN，β∈（VN ∪ VT）+
- 或者为 S→ε，且S不出现再任何产生式的右边
定理2.
- 如果G=（VN，VT，P，S)是一个上下文有关文法，则存在另一个上下文有关文法G1，它所产生的语言与G相同，其中G1的开始符号不出现在G1的任何产生式的右边
- 如果G是一个上下文无关文法，也能找到一个上下文无关文法G1，如果G是一个正规文法，也能找到这样一个正规文法G1