一元函数微分学几何应用（二）-- 凹凸性与拐点

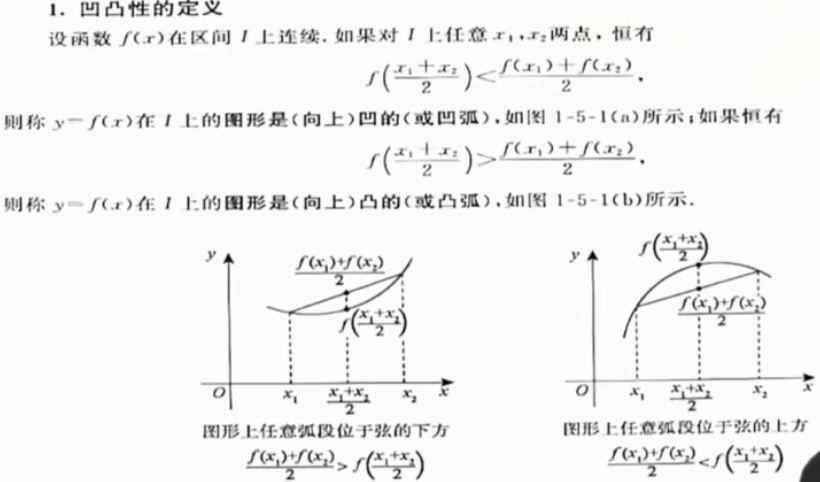
凹凸性

拐点

• 凸弧与凹弧的分界点
• 拐点在曲线上，写作 (x₀, f(x₀))
• 极值点在定义域上，写作 x₀

判别凹凸性

二阶可导点是拐点的必要条件

判别凹凸性的第一充分条件（左右邻域二阶导异号）

• x₀的某去心邻域内，二阶导数存在，在该点处二阶导两侧变号（由正变负，或由正变负），则点(x₀, f(x₀))为曲线上拐点

判别凹凸性的第二充分条件（二阶导数=0，三阶导数≠0）

• x₀的某去心邻域内三阶可导，且f‘’(x0)=0，f'''(x0)≠0，则(x0, f(x₀))为拐点
• 利用导数定义和保号性证明

判别凹凸性的第三充分条件

• f(x)在x₀处n阶可导，且 f^(m)(x₀)=0(m=2,...,n-1)，f⁽ⁿ⁾(x)≠0(n≥2)
• f'(x₀)=f''(x₀)=...=f^(n-1)(x₀)=0
  
• 若n为奇数且f⁽ⁿ⁾(x₀)=0，(x₀, f(x₀))为拐点
• 若n为奇数且f⁽ⁿ⁾(x₀)>0时，f(x)在x₀处取得极小值