题目描述
你准备给弟弟 Ike 买一件礼物,但是,Ike 挑选礼物的方式很特别:他只喜欢那些能被他排成有序形状的东西。
你准备给 Ike 买一个风铃。风铃是一种多层的装饰品,一般挂在天花板上。
每个风铃都包含一些由竖直线连起来的水平杆。每根杆的两头都有线连接,下面或者挂着另一根水平杆,或者挂着一个玩具。下面是一个风铃的例子:
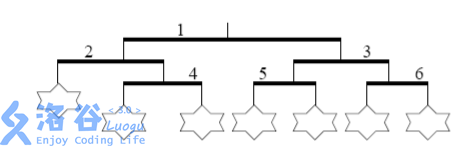
为了满足弟弟,你需要选一个满足下面两个条件的风铃:
(1) 所有的玩具都在同一层(也就是说,每个玩具到天花板之间的杆的个数是一样的)或至多相差一层。
(2) 对于两个相差一层的玩具,左边的玩具比右边的玩具要更靠下一点。
风铃可以按照下面的规则重新排列:任选一根杆,将杆两头的线“交换”。也就是解开一根杆左右两头的线,然后将它们绑到杆的另一头。这个操作不会改变更下面的杆上线的排列顺序。
正在训练信息学奥林匹克的你,决定设计一个算法,判断能否通过重新排列,将一个给定的风铃变为 Ike 喜欢的样子。
考虑上面的例子,上图中的风铃满足条件(1),却不满足条件(2)——最左边的那个玩具比它右边的要高。
但是,我们可以通过下面的步骤把这个风铃变成一个 Ike 喜欢的:
-
第一步,将杆 1 的左右两边交换,这使得杆 2 和杆 3 的位置互换,交换的结果如下图所示:
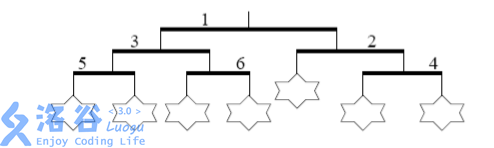
-
第二步,也是最后一步,将杆 2 的左右两边交换,这使得杆 4 到了左边,原来在左边的玩具到了右边,交换的结果发下图所示:
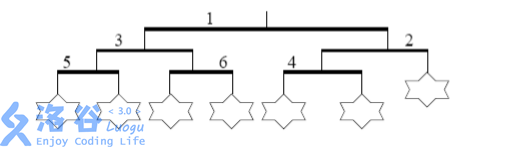
现在的这个风铃就满足 Ike 的条件了。
你的任务是:给定一个风铃的描述,求出最少需要多少次交换才能使这风铃满足 Ike 的条件(如果可能)
输入输出格式
输入格式:
输入的第一行包含一个整数 n(1≤n≤100 000),表示风铃中有多少根杆。
接下来的 n 行描述杆的连接信息。这部分的第 i 行包含两个由空格分隔的整数 li和 ri,描述杆 i 的左右两边悬挂的东西。如果挂的是一个玩具,则对应的值为-1,否则为挂在下面的杆的编号
输出格式:
输出仅包含一个整数。表示最少需要多少次交换能使风铃满足 Ike 的条件。如果不可能满足,输出-1。
输入输出样例
6 2 3 -1 4 5 6 -1 -1 -1 -1 -1 -1
2
首先对于所有玩具如果有深度差超过1的就是无解(显然),所以dfs一遍记录最小最大的深度即可。然后如果有一个点的两颗子树中都含有最小、最大深度,那么这种情况也是无解,因为无论你怎么交换都不能使深度小的全部到右边去。
然后考虑最少交换次数:其实对于每一个节点的左右子树,三种情况需要交换,
左边全是小深度的,右边全是大深度的
左边全是小深度的,右边大小深度都有
左边大小深度都有,右边全是大深度的
dfs搜一遍就好了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 int ans,maxdep,mindep,flag,ch[100001][2],n; 8 void dfs(int x,int dep) 9 { 10 if (x==-1) 11 { 12 maxdep=max(maxdep,dep); 13 mindep=min(mindep,dep); 14 return; 15 } 16 dfs(ch[x][0],dep+1); 17 dfs(ch[x][1],dep+1); 18 } 19 int solve(int now,int dep) 20 { 21 if (now==-1) 22 { 23 if (dep==mindep) return 0; 24 return 1; 25 } 26 int x=solve(ch[now][0],dep+1); 27 int y=solve(ch[now][1],dep+1); 28 if (x==0&&y==1) ans++; 29 if (x==2&&y==1) ans++; 30 if (x==0&&y==2) ans++; 31 if (x==2&&y==2) 32 { 33 flag=1; 34 return 2; 35 } 36 if (x==2||y==2) return 2; 37 if (x+y==1) return 2; 38 if (x+y==0) return 0; 39 return 1; 40 } 41 int main() 42 {int i; 43 cin>>n; 44 for (i=1;i<=n;i++) 45 { 46 scanf("%d%d",&ch[i][0],&ch[i][1]); 47 } 48 maxdep=0;mindep=1e9; 49 dfs(1,0); 50 if (maxdep-mindep>1) 51 { 52 cout<<-1; 53 return 0; 54 } 55 if (maxdep==mindep) 56 { 57 cout<<0; 58 return 0; 59 } 60 solve(1,0); 61 if (flag) 62 { 63 cout<<-1; 64 return 0; 65 } 66 cout<<ans; 67 }