题目背景
博弈正在机房颓一个叫做《模拟城市2.0》的游戏。
2048年,经过不懈努力,博弈终于被组织委以重任,成为D市市委书记!他勤学好问,励精图治,很快把D市建设成富强民主文明和谐的美好城市。为了进一步深化发展,他决定在海边建立一个经济开发区。
题目描述
已知开发区的建筑地块是一个n×nn imes nn×n的矩形,而开发区可以建造三种建筑: 商业楼,住宅楼,教学楼。这任何两座建筑可以堆叠,可以紧密相邻。他需要建造正好aaa座商业楼,bbb座住宅楼,ccc座教学楼。但是,城市建成后要应付检查,如果安排的太混乱会被批评。不过幸运的是,只有一条公路经过了该开发区的一侧,就是说,检察人员全程只能看到开发区的一面。
因此,他需要使得开发区建成后,从正面看去,只有一种类型的建筑。
一共有多少种满足条件的方案呢? 请输出方案数,并对109+710^9+7109+7取模。
注意,对于同一个nnn,会有多组数据。
输入输出格式
输入格式:第一行两个整数n,Tn,Tn,T
接下来T行,每行三个整数,表示该组数据的a,b,ca,b,ca,b,c
输出格式:输出共T行,每行一个整数:表示各数据答案取模109+710^9+7109+7的结果。
输入输出样例
说明
对于20%的数据,n≤2 a,b,c≤3 T≤5n leq 2 a,b,c leq 3 T leq 5n≤2 a,b,c≤3 T≤5
对于另外10%的数据,n≤3 a,b,c≤4 T≤5n leq 3 a,b,c leq 4 T leq 5n≤3 a,b,c≤4 T≤5
对于另外20%的数据,b=0b=0b=0
对于另外10%的数据,T≤10T leq 10T≤10
对于全部100%的数据,a,b,c,n≤25 T≤5×105a,b,c,n leq 25 T leq 5 imes 10^5a,b,c,n≤25 T≤5×105
样例1

样例2
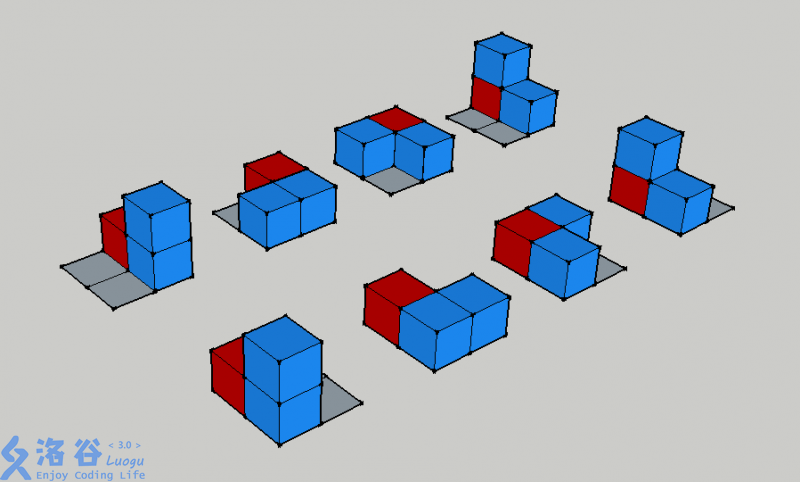
纵列和纵列之间不会相互遮挡,因此方案数很好统计。
所以我们需要处理出纵列合法的方案数。
虽然有三种方块,但我们只是需要一种漏在外面,所以可以把另外两种先不考虑
令f[i][j][k][x][y]为第i格,高度为j,最高为k,可见的方格为x,不可见为y的方案数
放到下一格:
1 f[i+1][0][k][x][y]+=f[i][k][k][x][y];
放到上面:
1 if (j==k) 2 f[i][j+1][k+1][x+1][y]+=f[i][j][k][x][y]; 3 else 4 f[i][j+1][k][x+1][y]+=f[i][j][k][x][y], 5 f[i][j+1][k][x][y+1]+=f[i][j][k][x][y];
现在我们处理出了一列的方案数
g[x][y]表示∑f[n][0][i][x][y]
那么对于一列,我们求出了可见数x,不可见数y的方案数
接下来考虑行,因为列之间不影响
dp[i][j][k]表示第i列可见数j,不可见数k的方案数
dp[i+1][x+j][y+k]+=dp[i][j][k]*g[x][y]
如果只让一种(如住宅楼)能看见,那么方案数已经显而易见了。
1 dp[n][a][b+c]*C[c+b][b];
那么最终答案就呼之欲出了。
1 ans=(dp[n][a][b+c]*C[b+c][b])+(dp[n][b][c+a]*C[c+a][c])+(dp[n][c][a+b]*C[a+b][a]);
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 typedef long long lol; 7 lol f[27][27][27][27][54],dp[27][27][54],C[54][54],g[54][54],ans; 8 lol Mod=1000000007; 9 int n,T; 10 int main() 11 {int i,j,k,x,y,a,b,c; 12 cin>>n>>T; 13 f[0][0][0][0][0]=1; 14 for (i=0;i<n;i++) 15 { 16 for (j=0;j<=25;j++) 17 { 18 for (k=j;k<=25;k++) 19 { 20 for (x=k;x<=25;x++) 21 { 22 for (y=0;y<=50;y++) 23 if (f[i][j][k][x][y]) 24 {//cout<<f[i][j][k][x][y]<<endl; 25 lol s=f[i][j][k][x][y]; 26 f[i+1][0][k][x][y]+=s,f[i+1][0][k][x][y]%=Mod; 27 if (j==k) 28 f[i][j+1][k+1][x+1][y]+=s,f[i][j+1][k+1][x+1][y]%=Mod; 29 else 30 { 31 f[i][j+1][k][x+1][y]+=s,f[i][j+1][k][x+1][y]%=Mod; 32 f[i][j+1][k][x][y+1]+=s,f[i][j+1][k][x][y+1]%=Mod; 33 } 34 } 35 } 36 } 37 } 38 } 39 for (i=0;i<=25;i++) 40 for (x=i;x<=25;x++) 41 for (y=0;y<=50;y++) 42 g[x][y]+=f[n][0][i][x][y],g[x][y]%=Mod; 43 dp[0][0][0]=1; 44 for (i=0;i<n;i++) 45 { 46 for (j=0;j<=25;j++) 47 { 48 for (k=0;k<=50;k++) 49 if (dp[i][j][k]) 50 {//cout<<dp[i][j][k]<<endl; 51 for (x=0;j+x<=25;x++) 52 for (y=0;k+y<=50;y++) 53 { 54 dp[i+1][j+x][k+y]+=dp[i][j][k]*g[x][y]%Mod; 55 dp[i+1][j+x][k+y]%=Mod; 56 } 57 } 58 } 59 } 60 C[0][0]=1; 61 for(i=1;i<=50;i++) 62 { 63 C[i][0]=1; 64 for(j=1;j<=i;j++) 65 { 66 C[i][j]=C[i-1][j-1]+C[i-1][j]; 67 if (C[i][j]>=Mod) C[i][j]-=Mod; 68 } 69 } 70 while (T--) 71 { 72 scanf("%d%d%d",&a,&b,&c); 73 //cout<<dp[n][a][b+c]<<' '<<dp[n][b][a+c]<<' '<<dp[n][c][a+b]<<endl; 74 ans=((dp[n][a][b+c]*C[b+c][b]%Mod)+(dp[n][b][a+c]*C[a+c][a]%Mod)+(dp[n][c][a+b]*C[a+b][a]%Mod))%Mod; 75 printf("%lld ",ans); 76 } 77 }