【题目描述】
SAT(Satisfiability,可满足性)问题是著名的 NP 完全问题,它的内容是:判断由有限个
布尔变量及其“非”用“或”操作连接起来的表达式组是否可以都为 TRUE。
2-SAT 问题对 SAT 问题做了如下限制:每个表达式由两个变量构成。
XOR-SAT 问题对 SAT 问题做了如下限制:表达式仅由变量与“异或”操作构成。
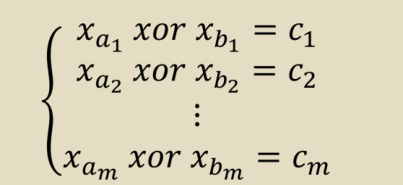
2-XOR-SAT 问题包含了以上两个限制,即:有 n 个布尔变量?1 …?? 与 m 个双变量
异或方程
你需要判断方程组是否有解,如果有解请输出任意一组解,否则输出无解。
【输入文件】
第一行两个整数 n m
接下来m行,每行两个整数 a? b? 及一个大写字符串 c? ,c? 为”TRUE”或”FALSE”
【输出文件】
若无解,则输出一行”Impossible”
若有解,则第一行输出”Possible”,接下来?行输出?1 …?? 的值”TRUE”或”FALSE”
【样例输入】
3 2
1 2 TRUE
2 3 FALSE
【样例输出】
Possible
FALSE
TRUE
TRUE
【数据范围】
30%的数据保证 n ≤ 20;m ≤ 20
100%的数据保证 1 ≤ n ≤ 100,000;1 ≤ m ≤ 100,000
考虑把不同的x连边,相同u,v的转换
可以理解u与v+n不同,u+n与v不同
一个点i与i+n显然不同
然后就可以黑白染色
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 struct Node 8 { 9 int next,to; 10 } edge[800001]; 11 int num,head[200001],n,m; 12 int vis[200001]; 13 char s[201]; 14 void add(int u,int v) 15 { 16 num++; 17 edge[num].next=head[u]; 18 head[u]=num; 19 edge[num].to=v; 20 } 21 bool dfs(int x,int col) 22 {int i; 23 vis[x]=col; 24 for (i=head[x];i;i=edge[i].next) 25 { 26 int v=edge[i].to; 27 if (vis[v]==-1) 28 { 29 dfs(v,col^1); 30 } 31 else if (vis[v]==vis[x]) 32 { 33 cout<<"Impossible "; 34 exit(0); 35 } 36 } 37 } 38 int main() 39 { 40 int u,v,i; 41 cin>>n>>m; 42 for (i=1;i<=n;i++) 43 add(i,n+i),add(n+i,i); 44 for (i=1; i<=m; i++) 45 { 46 scanf("%d%d%s",&u,&v,s); 47 if (s[0]=='F') 48 { 49 add(v+n,u); 50 add(u,v+n); 51 add(u+n,v); 52 add(v,u+n); 53 } 54 else if (s[0]=='T') 55 { 56 add(u,v); 57 add(v,u); 58 } 59 } 60 memset(vis,-1,sizeof(vis)); 61 for (i=1; i<=n; i++) 62 if (vis[i]==-1) 63 { 64 dfs(i,1); 65 } 66 cout<<"Possible"<<endl; 67 for (i=1;i<=n;i++) 68 if (vis[i]==1) printf("TRUE "); 69 else printf("FALSE "); 70 }