题目描述
丽江河边有n 家很有特色的客栈,客栈按照其位置顺序从 1 到n 编号。每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。
两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过 p 。
他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过 p元的咖啡店小聚。
输入输出格式
输入格式:
输入文件hotel.in,共n+1 行。
第一行三个整数n ,k ,p,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;
接下来的n 行,第 i+1 行两个整数,之间用一个空格隔开,分别表示 i 号客栈的装饰色调和i 号客栈的咖啡店的最低消费。
输出格式:
输出文件名为hotel.out 。
输出只有一行,一个整数,表示可选的住宿方案的总数。
输入输出样例
5 2 3 0 5 1 3 0 2 1 4 1 5
3
说明
【输入输出样例说明】
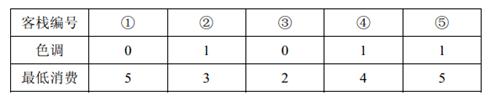
2 人要住同样色调的客栈,所有可选的住宿方案包括:住客栈①③,②④,②⑤,④⑤,但是若选择住4 、5 号客栈的话,4 、5 号客栈之间的咖啡店的最低消费是4 ,而两人能承受的最低消费是3 元,所以不满足要求。因此只有前 3 种方案可选。
【数据范围】
对于30% 的数据,有 n ≤100;
对于50% 的数据,有 n ≤1,000;
对于100%的数据,有 2 ≤n ≤200,000,0<k ≤50,0≤p ≤100 , 0 ≤最低消费≤100。
那么我们第一层循环枚举二号客人入住的客栈i时,一号客人只可能住在1....i-1,那么我们这么考虑,
如果与二号客人入住的客栈颜色相同的最近的客栈之间存在一个小于p的客栈,那么当前二号客人入住的客栈前面所有颜色与i相同的客栈都是一方案。
如果不存在,那么二号客人选择当前客栈的方案数就等于二号客人选择最近的那个客栈的方案数相等
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int pre[200001],cnt[200001],c[200001]; 7 int n,k,p; 8 int main() 9 { 10 cin>>n>>k>>p; 11 int cost=0,ans=0; 12 for (int i=1;i<=n;i++) 13 { 14 int color,val; 15 scanf("%d%d",&color,&val); 16 int j=pre[color]; 17 if (val<=p)cost=i; 18 if (j<=cost)c[i]=cnt[color]; 19 else c[i]=c[j]; 20 ans+=c[i]; 21 pre[color]=i; 22 cnt[color]++; 23 } 24 printf("%d",ans); 25 }