【模板】树状数组 2

//洛谷P3368

对于树状数组这个数据结构，维护的无非就是这几个操作：

1.单点修改，区间求和

2.区间修改，单点查询

对于这道题，就是操作2

（对于树状数组的基础与操作1的实现，请见http://www.cnblogs.com/XjzLing/p/7943547.html）

对于这道题，我们要引入差积数组的概念：

差积数组首先满足d[0]=a[0]，然后d[i]=a[i]-a[i-1]。

这样的话，一个点的差积数组的前缀和，就是这个数的值，这就方便了O(logn)的查询。

首先，对于区间修改：

 

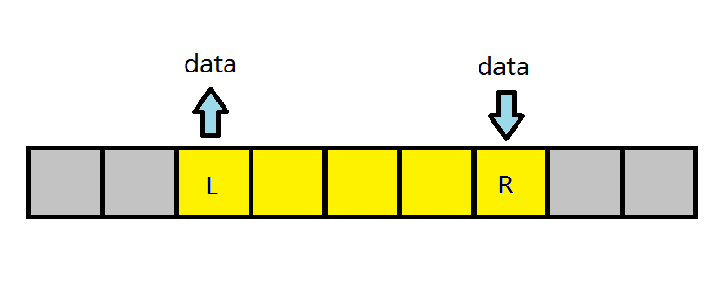
先将L位置的值加上data，再将R位置的值减去data。这样，在查询[L,R]区间内的前缀值时，所得的结果就会加上data，在查询[R,n]的位置时，结果就不会有变化了：

if(opr==1) {
            scanf("%d%d%d",&l,&r,&data);
            update(l,data);
            update(r+1,-data);
        }

（剩下的内容与树状数组1的内容完全一样：http://www.cnblogs.com/XjzLing/p/7943547.html）

下面粘上代码：

#include<algorithm>
#include<iostream>
#include<string>
#include<cstdio>
#include<map>
#define maxn 500000 +10
using namespace std;
int n,m,p;
int opr,l,r;
int a[maxn];
int d[maxn];
int lowbit(int x){
    return x&-x;
}
void update(int pos,int data){
    while(pos<=n){
        d [pos]+=data;
        pos+=lowbit(pos);
    }
}
int query(int pos){
    int ans=0;
    while(pos>0){
        ans+=d[pos];
        pos-=lowbit(pos);
    }
    return ans;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) update(i,a[i]-a[i-1]);
    for(int i=1;i<=m;i++){
        scanf("%d",&opr);
        int data;
        if(opr==1) {
            scanf("%d%d%d",&l,&r,&data);
            update(l,data);
            update(r+1,-data);
        }
        else {
            scanf("%d",&r);
            printf("%d
",query(r));
        }
    }
    return 0;
}