//洛谷P3374
对于树状数组这个数据结构,维护的无非就是这几个操作:
1.单点修改,区间求和
2.区间修改,单点查询
对于这道题,就是操作1
首先,我们先来了解一下树状数组:
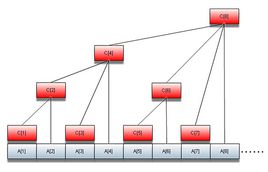
在上图中A数组是原数组,C数组记录了其所有儿子结点的和,如何知道C[i]的父亲的位置呢?
这就要引入lowbit函数了:
int lowbit(int x){ return x&-x; }
这个函数的返回值其实就是函数对象与上它取反在+1的值,想找规律的同学们不仿自己动手算一算,找一找规律。
不难发现,C[i]的父亲结点是C[i+lowbit(i)]所以这就完成了对于各个区间和的维护。
然后是单点修改的内容:update()
void update(int pos,int data){ while(pos<=n){ a[pos]+=data; pos+=lowbit(pos); } }
这个函数对于某个位置pos,增加数值data,将pos结点的父亲结点,父亲的父亲结点......祖先都进行修改。
这就可以用O(logn)的时间进行一次前缀和的维护。
查询的操作就简单多了:query()
int query(int pos){ int ans=0; while(pos>0){ ans+=a[pos]; pos-=lowbit(pos); } return ans; }
这样可以用O(logn)的时间进行一次前缀和的查询。
最后对于结果[l,r]的查询,只需要用query(r)-query(l)就可以了
下面是代码整合:
#include<algorithm> #include<iostream> #include<string> #include<cstdio> #include<map> #define maxn 500000 +10 using namespace std; int n,m,p; int opr,l,r; int a[maxn]; int lowbit(int x){ return x&-x; } void update(int pos,int data){ while(pos<=n){ a[pos]+=data; pos+=lowbit(pos); } } int query(int pos){ int ans=0; while(pos>0){ ans+=a[pos]; pos-=lowbit(pos); } return ans; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ scanf("%d",&p); update(i,p); } for(int i=1;i<=m;i++){ scanf("%d%d%d",&opr,&l,&r); if(opr==1) update(l,r); else printf("%d ",query(r)-query(l-1)); } return 0; }