【题解】Alyona and Triangles [CF682E]

【题解】Alyona and Triangles [CF682E]

传送门：( ext{Alyona and Triangles}) ( ext{[CF682E]})

【题目描述】

二维平面上给定 (n) 个点， 满足从中任取 (3) 个点所构成的三角形的面积都不超过 ( ext{S}) 。

要求构造一个三角形覆盖这 (n) 个点，并且面积不超过 ( ext{4S}) 。三角形顶点可以取二维平面上的任意整数坐标。

【分析】

【学习笔记】计算几何全家桶

计算几何水题（毒瘤程度不及 SCOI 的万分之一）。

经过一番手推+盲猜，发现一个性质：先求出在这 (n) 个点中任取三个点所能构成的最大三角形，然后将其扩大成原来的四倍即为答案（分别以三条边作为对角线画四边形所并成的大三角）。

如样例，红色部分为求出的最大三角，对其进行扩展得到答案（蓝色大三角）：

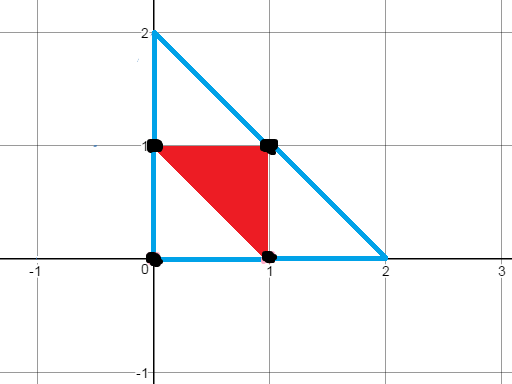
易证所有点都一定会被包含在大三角中（如果在外面还有其他点，那么红三角就一定不是最大的，前后矛盾）。

于是问题转换为：用给定点构造一个最大三角形。

可知最大三角的顶点都在凸包上，直接暴力枚举一条边，用类似旋转卡壳的方法求出距离该直线最远的点，然后取最大的一个即可。

【Code】

#include<algorithm>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Vector Point
#define Re register int
using namespace std;
const int N=5e3+3;
int n;LL S;
const LD eps=1e-8;
inline int dcmp(LD a){return a<-eps?-1:(a>eps?1:0);}//处理精度
struct Point{
    LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
    inline void in(){scanf("%lf%lf",&x,&y);}
    inline void print(){printf("%.lf %.lf
",x,y);}
}A,B,C,P[N],cp[N];
inline LD Cro(Vector a,Vector b){return a.x*b.y-a.y*b.x;}//【叉积】
inline Vector operator+(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
inline Vector operator-(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
inline bool cmp(Point a,Point b){return a.x!=b.x?a.x<b.x:a.y<b.y;}//按坐标排序
inline int ConvexHull(Point *P,Re n,Point *cp){//【Graham扫描法】求凸包
    sort(P+1,P+n+1,cmp);
    Re t=0;
    for(Re i=1;i<=n;++i){//下凸包
        while(t>1&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
        cp[++t]=P[i];
    }
    Re St=t;
    for(Re i=n-1;i>=1;--i){//上凸包
        while(t>St&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
        cp[++t]=P[i];
    }
    return --t;//要减一
}
int main(){
//    freopen("123.txt","r",stdin);
    scanf("%d%lld",&n,&S);
    for(Re i=1;i<=n;++i)P[i].in();
    Re cnt=ConvexHull(P,n,cp);
    LD Max=0;
    for(Re i=1;i<=cnt;++i)//枚举三角形一条边cp[i]cp[j]
        for(Re j=i+1,k=j<cnt?j+1:1;j<=cnt&&k!=i;++j){
            while(dcmp(Cro(cp[j]-cp[i],cp[k]-cp[i])-Cro(cp[j]-cp[i],cp[k+1]-cp[i]))<0)k=k<cnt?k+1:1;
            if(k!=i&&k!=j){
                LD tmp=Cro(cp[j]-cp[i],cp[k]-cp[i]);//计算三角形面积
                if(tmp>Max)Max=tmp,A=cp[i],B=cp[j],C=cp[k];
            }
        }
    (A-C+B).print(),(B-A+C).print(),(C-B+A).print();
}