【题解】CIRU - The area of the union of circles [SP8073] 圆的面积并 [Bzoj2178]
传送门:
【题目描述】
给出 (n) 个圆的圆心坐标 ((x,y)) 和半径 (r),求它们覆盖的总面积。
【输入】
第一行一个整数 (n),表示一共有 (n) 个圆,接下来 (n) 行每行三个整数 (x,y,r) 。
【输出】
答案保留三位小数。
【样例】
样例输入:
3
0 0 1
0 0 1
100 100 1
样例输出:
6.283
【数据范围】
(100 \%:) (1 leqslant n leqslant 1000,) (|x|,|y| leqslant 1000,) (0 leqslant r leqslant 1000)
【分析】
圆面积并的板题。
【前置芝士】
自适应辛普森积分 (乱搞)。
虽然不知道积分是什么东西,但老师说只要背了公式而且会用它求面积就可以了:(ans(l,r)=frac{(r-l)(F_l+4F_{mid}+F_r)}{6}) 。
当计算平面图形面积时,(F_Y) 就是直线 (y=Y) 穿过图形的部分的长度。
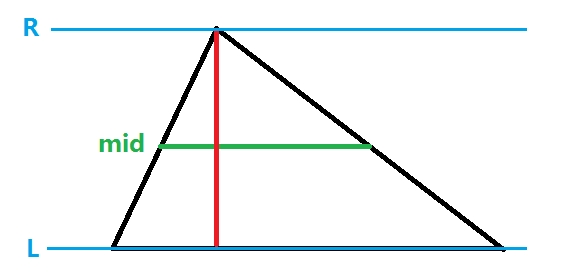
例:一个底为 (a),高为 (h) 的三角形面积可表示为: (S=frac{h*(a+4*frac{a}{2}+0)}{6}=frac{a*h}{2}) 。如下图,(r-l=h,F_l=a,F_{mid}=frac{a}{2},F_r=0):
(另外,当计算立体图形体积时,(F_Y) 就是平面 (z=Y) 穿过图形的部分的面积。例:一个半径为 (r) 的球体积可表示为: (V=frac{2r*(0+4pi r^2+0)}{6}=frac{4pi r^3}{3}) )
但并不是所有的图形都可以这样子做,比如在求圆面积时就会出问题(设半径为 (r)): (S=frac{2r*(0+4*2r+0)}{6}=frac{4 r^2}{3} eq pi r^2) 。
这时候就需要用到自适应辛普森法:分别用公式出 (ans(l,mid)) 和 (ans(mid,r)),若二者之和与 (ans(l,r)) 的差值小于 (eps),则返回 (ans(l,r)),否则递归求解 ((l,mid)) 与 ((mid,r)) 再加起来。
代码如下:
#define LD double
#define Rd register LD
inline LD F(Rd Y){return ???;}//视情况而定
inline LD Simpson(Rd L,Rd R){return (R-L)*(F(L)+4.0*F((L+R)*0.5)+F(R))/6.0;}//套公式
inline LD sakura(Rd L,Rd R,Rd now){//求解ans(L,R)
Rd mid=(L+R)*0.5,FL=Simpson(L,mid),FR=Simpson(mid,R);//先用公式求左右两边
if(!dcmp(now-FL-FR))return now;//满足精度要求
return sakura(L,mid,FL)+sakura(mid,R,FR);//递归求解并求和
}
【问题求解】
回到这道题,求出最靠边上的两端点 (Y_{min},Y_{max}) 直接递归求解即可,至于上面的 (F) 函数可以暴力枚举所有圆求交弦,然后对其排序做线段覆盖。
注意精度要调好,( ext{Bzoj}) 需要 (1e!-!13),( ext{SPOJ}) 需要 (1e!-!7) 。
时间复杂度: (O( nlogn imes) 玄学 ()) 。其中 “玄学” 为 (F) 函数调用次数。
【优化】
只是单纯地求解 ((Y_{min},Y_{max})) 会被 ( ext{Bzoj}) 的 【变态毒瘤数据】 卡掉,( ext{SPOJ}) 也过不了。
为什么?
如果有 (1) 个孤零零的圆在最上面,(999) 个圆堆在最下面,最后算出来误差会非常大,所以要分段处理,即将所有圆划分为若干个联通块分别求解(可以将每个圆的上下端点连起来跑线段覆盖),这样子误差会小一些。
此时【变态毒瘤数据】成功地算了出来,但花了 (30s),考虑对 (F) 函数进行记忆化,再经过一波卡常,本机 (10.6s),交上去刚好卡过。
【再优化】
那么,连 【八聚氧】 都救不了的 ( ext{SPOJ}) 又该怎么办呢?
提前预处理出大圆包含小圆的情况(把被包含的小圆删掉),大大减小 (nlogn) 部分的消耗。
呼呼,终于过了
【Code】
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<map>
#define LD double
#define LL long long
#define Re register int
#define Rd register LD
#define Vector Point
using namespace std;
const int N=2003;
const LD eps=1e-13;
int n,m;map<LD,LD>vis;
inline int dcmp(Rd a){return a<-eps?-1:(a>eps?1:0);}
struct Point{
LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
inline void in(){scanf("%lf%lf",&x,&y);}
};
struct Segment{
LD L,R;Segment(LD l=0,LD r=0){L=l,R=r;}
inline bool operator<(Segment O)const{return L!=O.L?L<O.L:R<O.R;}
}Seg[N];
struct Circle{
LD x,y,r,L,R,D,U;
inline void in(){scanf("%lf%lf%lf",&x,&y,&r),L=x-r,R=x+r,D=y-r,U=y+r;}
inline bool operator<(Circle B)const{return D<B.D;}//按下端点排序
}C[N],C_[N];
inline bool cmp(Circle A,Circle B){return A.r<B.r;}//按半径排序
inline LD dis(Circle A,Circle B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}
inline LD SS(Rd x){return x*x;}
inline LD F(Rd Y){
if(vis[Y])return vis[Y];//记忆化
Re t=0;Rd ans=0;
for(Re i=1;i<=n;++i)
if(dcmp(Y-C[i].D)>0&&dcmp(Y-C[i].U)<0){//如果直线穿过了该圆
Rd tmp=sqrt(SS(C[i].r)-SS(C[i].y-Y));//勾股定理求交弦
if(dcmp(tmp)>0)Seg[++t]=Segment(C[i].x-tmp,C[i].x+tmp);
}
if(!t)return 0.0;
sort(Seg+1,Seg+t+1);
for(Re i=1,j;i<=t;i=j+1){
Rd L=Seg[i].L,R=Seg[i].R;j=i;
while(j<t&&Seg[j+1].L<=R)++j,R=max(R,Seg[j].R);
ans+=R-L;
}
return vis[Y]=ans;
}
inline LD Simpson(Rd L,Rd R){return (R-L)*(F(L)+4.0*F((L+R)*0.5)+F(R))/6.0;}//【辛普森公式】
inline LD sakura(Rd L,Rd R,Rd now){//【自适应】
Rd mid=(L+R)*0.5,FL=Simpson(L,mid),FR=Simpson(mid,R);
if(!dcmp(now-FL-FR))return now;
return sakura(L,mid,FL)+sakura(mid,R,FR);
}
LD ans;
int main(){
// freopen("789.txt","r",stdin);
scanf("%d",&m);
for(Re i=1;i<=m;++i)C_[i].in();
sort(C_+1,C_+m+1,cmp),C[++n]=C_[m];//按半径大小排序
for(Re i=m-1;i>=1;--i){//【大圆吃小圆】从大圆向小圆枚举
Re flag=1;
for(Re j=1;j<=n&&flag;++j)
if(dcmp(C_[i].r-C[j].r+dis(C_[i],C[j]))<=0)flag=0;//小r+大r <= dis,则说明小圆C_[i]被包含了在了C[j]以内
if(flag)C[++n]=C_[i];//C_[i]没有被大圆包含
}
sort(C+1,C+n+1);
for(Re i=1,j;i<=n;i=j+1){//【分段处理】每个联通块单独处理
Rd D=C[i].D,U=C[i].U;j=i;
while(j<n&&C[j+1].D<=U)++j,U=max(U,C[j].U);
ans+=sakura(D,U,Simpson(D,U));
}
printf("%.3lf",ans);
}