【题解】The Great Divide [Uva10256]
传送门:( ext{The Great Divide [Uva10256]})
【题目描述】
输入多组数据,每组数据给定 (n) 个红点坐标和 (m) 个蓝点坐标,判断是否可以用一条直线将两种颜色的点完全隔离开(直线不能经过某个点)。
【输入】
每组数据第一行为两个整数 (n,m),接下来 (n+m) 行每行两个整数 (x,y) 表示一个坐标,前 (n) 行为红点,后 (m) 行表示蓝点。
【输出】
如果存在这样一条直线输出 (Yes),否则输出 (No) 。
【样例】
样例输入:
4 3
100 600
200 400
600 500
300 700
400 100
600 200
500 300
4 3
100 600
400 100
600 200
500 300
200 400
600 500
300 700
0 0
样例输出:
Yes
No
【数据范围】
(100\%:) (1leqslant n,m leqslant 500,) (-1000 leqslant x,y leqslant 1000)
【分析】
凡是遇到计算几何的题目,先画张图出来:
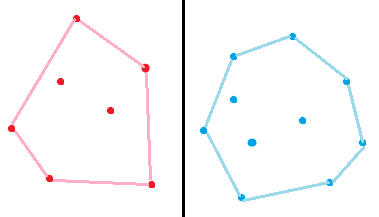
观察发现:如果存在一条合法直线,两部分点的凸包必定相离。
两多边形相离的条件有:
((1).) 属于不同多边形的任意两边都不相交。
((2).) 一个多边形上的任意点都不被另一个多边形所包含。
求凸包可以 (O(n)) 解决,由于数据范围比较小,暴力枚举两个凸包进行判断就可以了。
判断线段相交为 (O(1)),(PIP) 可以用 (O(n)) 的射线法或者转角法,由于这里判断的是凸包,所以也可以用 (O(logn)) 的二分法,只是要注意凸包点集的顺序是顺时针还是逆时针,这里 (WA) 了无数遍。
时间复杂度为 (O(n^3)/O(n^2logn)) 。
【Code】
【射线法】
#include<algorithm>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Vector Point
#define Re register int
using namespace std;
const int N=1e5+3;
const LD eps=1e-8;
int n,T;
inline int dcmp(LD a){return a<-eps?-1:(a>eps?1:0);}
struct Point{
LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
inline void in(){scanf("%lf%lf",&x,&y);}
};
inline LD Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
inline LD Cro(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
inline LD Len(Vector a){return sqrt(Dot(a,a));}
inline LD Angle(Vector a,Vector b){return acos(Dot(a,b)/Len(a)/Len(b));}
inline Point operator+(Point a,Vector b){return Point(a.x+b.x,a.y+b.y);}
inline Vector operator-(Point a,Point b){return Vector(a.x-b.x,a.y-b.y);}
inline Vector operator*(Vector a,LD x){return Vector(a.x*x,a.y*x);}
inline int pan_cross_LL(Point a,Point b,Point c,Point d){//判断两线段AB,CD是否相交
LD c1=Cro(b-a,c-a),c2=Cro(b-a,d-a);
LD d1=Cro(d-c,a-c),d2=Cro(d-c,b-c);
return dcmp(c1)*dcmp(c2)<=0&&dcmp(d1)*dcmp(d2)<=0;//这里重合也要算
}
inline bool cmp1(Point a,Point b){return a.x==b.x?a.y<b.y:a.x<b.x;};//按坐标排序
struct Poly{
int n,cnt;Point cp[N],Poi[N];
inline int ConvexHull(Point *P,Re n,Point *cp){
sort(P+1,P+n+1,cmp1);
Re t=0;
for(Re i=1;i<=n;++i){//下凸包
while(t>1&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
Re St=t;
for(Re i=n-1;i>=1;--i){//上凸包
while(t>St&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
return --t;//要减一
}
inline void sakura(){
for(Re i=1;i<=n;++i)Poi[i].in();
cnt=ConvexHull(Poi,n,cp);
}
}A,B;
inline int pan_PL(Point p,Point a,Point b){//判断点P是否在线段AB上
return !dcmp(Cro(p-a,b-a))&&min(a.x,b.x)<=p.x&&p.x<=max(a.x,b.x)&&min(a.y,b.y)<=p.y&&p.y<=max(a.y,b.y);
}
inline int PIP(Point *P,Re n,Point a){
Re cnt=0;LD tmp;
for(Re i=1;i<=n;++i){
Re j=i<n?i+1:1;
if(pan_PL(a,P[i],P[j]))return 2;//点在多边形上
if(a.y>=min(P[i].y,P[j].y)&&a.y<max(P[i].y,P[j].y))//纵坐标在该线段两端点之间
tmp=P[i].x+(a.y-P[i].y)/(P[j].y-P[i].y)*(P[j].x-P[i].x),cnt+=dcmp(tmp-a.x)>0;//交点在A右方
}
return cnt&1;//穿过奇数次则在多边形以内
}
inline int judge(){
for(Re i1=1;i1<=A.cnt;++i1){
Re j1=i1<A.cnt?i1+1:1;
for(Re i2=1;i2<=B.cnt;++i2){
Re j2=i2<B.cnt?i2+1:1;
if(pan_cross_LL(A.cp[i1],A.cp[j1],B.cp[i2],B.cp[j2]))return 0;//两线段相交
if(PIP(B.cp,B.cnt,A.cp[i1])||PIP(A.cp,A.cnt,B.cp[i2]))return 0;//点包含在内
}
}
return 1;
}
int main(){
// freopen("123.txt","r",stdin);
while(scanf("%d%d",&A.n,&B.n)&&A.n&&B.n)A.sakura(),B.sakura(),puts(judge()?"Yes":"No");
}
【二分法】
#include<algorithm>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Vector Point
#define Re register int
using namespace std;
const int N=1e5+3;
const LD eps=1e-8;
int n,T;
inline int dcmp(LD a){return a<-eps?-1:(a>eps?1:0);}
struct Point{
LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
inline void in(){scanf("%lf%lf",&x,&y);}
};
inline LD Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
inline LD Cro(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
inline LD Len(Vector a){return sqrt(Dot(a,a));}
inline LD Angle(Vector a,Vector b){return acos(Dot(a,b)/Len(a)/Len(b));}
inline Point operator+(Point a,Vector b){return Point(a.x+b.x,a.y+b.y);}
inline Vector operator-(Point a,Point b){return Vector(a.x-b.x,a.y-b.y);}
inline Vector operator*(Vector a,LD x){return Vector(a.x*x,a.y*x);}
inline int pan_cross_LL(Point a,Point b,Point c,Point d){//判断两线段AB,CD是否相交
LD c1=Cro(b-a,c-a),c2=Cro(b-a,d-a);
LD d1=Cro(d-c,a-c),d2=Cro(d-c,b-c);
return dcmp(c1)*dcmp(c2)<=0&&dcmp(d1)*dcmp(d2)<=0;//这里重合也要算
}
inline bool cmp1(Point a,Point b){return a.x==b.x?a.y<b.y:a.x<b.x;};//按坐标排序
struct Poly{
int n,cnt;Point cp[N],Poi[N];
inline int ConvexHull(Point *P,Re n,Point *cp){
sort(P+1,P+n+1,cmp1);
Re t=0;
for(Re i=1;i<=n;++i){//下凸包
while(t>1&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
Re St=t;
for(Re i=n-1;i>=1;--i){//上凸包
while(t>St&&dcmp(Cro(cp[t]-cp[t-1],P[i]-cp[t-1]))<=0)--t;
cp[++t]=P[i];
}
return --t;//要减一
}
inline void sakura(){
for(Re i=1;i<=n;++i)Poi[i].in();
cnt=ConvexHull(Poi,n,cp);
for(Re i=1;i<=cnt/2;++i)swap(cp[i],cp[cnt-i+1]);//这里求出来的凸包点集按逆时针排列,转换一下
}
}A,B;
inline int pan_PL(Point p,Point a,Point b){//判断点P是否在线段AB上
return !dcmp(Cro(p-a,b-a))&&min(a.x,b.x)<=p.x&&p.x<=max(a.x,b.x)&&min(a.y,b.y)<=p.y&&p.y<=max(a.y,b.y);
}
inline int judge(Point a,Point L,Point R){//判断点AL是否在AR右边
return dcmp(Cro(L-a,R-a))>0;//必须严格以内
}
inline int PIP(Point *P,Re n,Point a){//判断点A是否在凸多边形Poly以内(二分法)
//点按顺时针给出
if(judge(P[1],P[2],a)||judge(P[1],a,P[n]))return 0;//在P[1_2]或P[1_n]外
if(pan_PL(a,P[1],P[2])||pan_PL(a,P[1],P[n]))return 1;//在P[1_2]或P[1_n]上
Re L=2,R=n-1;
while(L<R){//二分找到一个位置pos使得P[1]_A在P[1_pos],P[1_(pos+1)]之间
Re mid=L+R+1>>1;
if(judge(P[1],a,P[mid]))L=mid;
else R=mid-1;
}
if(judge(P[L],P[L+1],a))return 0;//在P[pos_(pos+1)]外
if(pan_PL(a,P[L],P[L+1]))return 1;//在P[pos_(pos+1)]上
return 1;
}
inline int judge(){
for(Re i1=1;i1<=A.cnt;++i1){
Re j1=i1<A.cnt?i1+1:1;
for(Re i2=1;i2<=B.cnt;++i2){
Re j2=i2<B.cnt?i2+1:1;
if(pan_cross_LL(A.cp[i1],A.cp[j1],B.cp[i2],B.cp[j2]))return 0;//两线段相交
if(PIP(B.cp,B.cnt,A.cp[i1])||PIP(A.cp,A.cnt,B.cp[i2]))return 0;//点包含在内
}
}
return 1;
}
int main(){
// freopen("123.txt","r",stdin);
while(scanf("%d%d",&A.n,&B.n)&&A.n&&B.n)A.sakura(),B.sakura(),puts(judge()?"Yes":"No");
}