【题解】Dvoniz [COCI2011]
传送门:( ext{Dvoniz [COCI2011] [P5922]})
数据 由 ( ext{COCI}) 官网 提供。
【题目描述】
对于一个长度为 (2 imes K) 的序列,如果它的前 (K) 个元素之和小于等于 (S) 且后 (K) 个之和也小于等于 (S),我们则称之为 ( ext{interesting})。现给定一个长度为 (N) 的序列 (a),要求输出以每个元素开头能找到的最长 ( ext{interesting}) 序列的长度。
【输入】
第一行两个整数 (N,S)。
接下来 (N) 行,每行一个正整数,第 (i) 行表示序列中的第 (i) 个元素 (a_i)。
【输出】
输出共 (N) 行,每行一个整数,第 (i) 行表示以 (a_i) 开头的最长的 ( ext{interesting})序列。如果不存在,则输出 (0)。
【样例】
样例输入:
5 10000
1
1
1
1
1
样例输出:
4
4
2
2
0
【数据范围】
(100 \%:) (2 leqslant N leqslant 10^5,) (1 leqslant S,a_i leqslant 2 imes 10^9)
【分析】
一道灰常 ( ext{interesting}) 的题。
蒟蒻英语差没有细看官方题解,貌似是 (O(nlogn)) 的 (set),我自己 (yy) 了一种 (O(n)) 的神奇算法。
设以 (a[i]) 为起点的最长合法序列的中点为 (mid_i)(前半段为 ([i,mid]),后半段为 ([mid+1,mid*2-i+1])),则 (ans_i=2(mid_{i}-i+1))。
假设现已求出了 (mid_{i-1}),考虑 (mid_i) 与之有何联系,是否可以继承,如图:
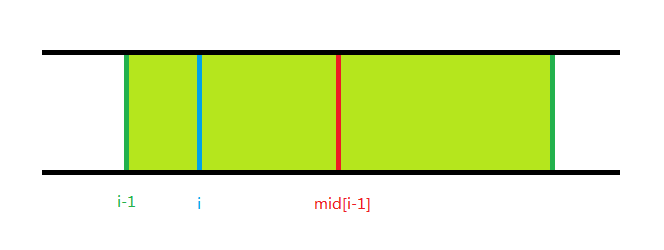
由于 (mid_{i-1}) 左右两边的绿色部分都小于等于 (S),那么向前推移了一位的 (i) 以 (mid_{i-1}) 为中点也可以构成合法序列,如下图(易知两边的蓝色部分都一定小于等于 (S) ):
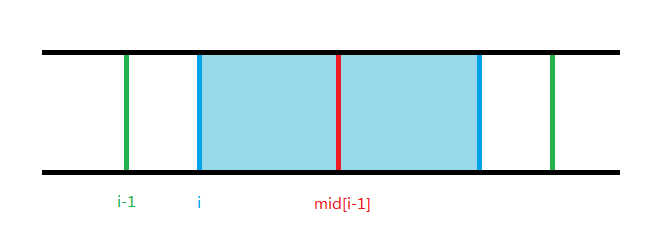
所以对于任意 (i in [2,n]),都有 (mid_{i-1} leqslant mid_{i}) 。
那么就可以用一个变量 (p) 来维护 (mid),从 (1) 开始不断地向后移动。
但有可能 (mid[i-1]) 并非是以 (a[i]) 开头的最优解,继续考虑对每个 (i) 求出最大的 (mid):
分开处理合法序列的左右两边,当 (i) 固定时,如果只看左边是否合法的话,那么从第一个不合法的位置开始,后面的都不合法(这不是理所当然的嘛),所以直接从 (mid_{i-1}) 开始向后暴力移动 (p)(也可以二分,但不便于后面的证明),扫到不合法的位置时就结束。此时在 ([mid_{i-1},p]) 中任取一个位置作为 (mid_{i}) 都可以满足序列左边合法,现在开始处理右边。
右边对于 (p) 的移动是不具有单调性的,那么就暴力往回移动 (p),找到第一个使得右边序列合法的位置,此时 (p) 停留的位置必定是 (mid_{i}) 的最优值。
暴力,暴力,全都是暴力。对于每次 (i) 都要把 (p) 向后移动若干位置再移回来,时间复杂度似乎为 (O(n^2)),但实际上是线性的,可以几十 (ms) 轻松跑过((n) 方过百万)。
【时间复杂度证明】
对于每个 (i),设 (p) 从 (mid_{i-1}) 开始向后移动了 (x_{i}),又从 (mid_{i-1}+x_{i}) 开始向前移回去了 (y_{i}),那么总时间复杂度可以表示为 (Theta=sum_{i=1}^{n} (x_{i}+y_{i})) —— ①。
对于每个 (i),(p) 从 (mid_{i-1}) 开始移动了 (x_{i}-y_{i}) 后到达了 (mid_{i}),那么 (mid_{i}) ((i in [1,n])) 的总移动距离就可以表示为 (sum_{i=1}^{n} (x_{i}-y_{i})) 。
又因为 (mid_{i}) 具有决策单调性,必定是从 (1) 移到 (n),所以总移动距离应为 (n),即:(n=sum_{i=1}^{n} (x_{i}-y_{i})) —— ②。
由于序列 ([mid_{i-1},mid_{i-1}+x_{i}]) 中元素之和一定是小于等于 (S) 的,那么取其中点 (M(mid_{i-1}+frac{x_{i}}{2})),一定可以使得 (M) 两边都合法,即 (mid_{i} geqslant M),于是有 (mid_{i-1}+x_{i}-y_{i} geqslant mid_{i-1}+frac{x_{i}}{2}),即 (y_{i} leqslant frac{x_{i}}{2}) —— ③。
由②③可知:
(n=sum_{i=1}^{n} (x_{i}-y_{i}) geqslant sum_{i=1}^{n} frac{x_{i}}{2}),即 (sum_{i=1}^{n} frac{3}{2}x_{i} leqslant 3n) 。
由①③可知:
(Theta=sum_{i=1}^{n} (x_{i}+y_{i}) leqslant sum_{i=1}^{n} frac{3}{2}x_{i}) 。
于是有 (Theta leqslant 3n) 。
时间复杂度得证,为 (O(n)) 。
(这样看来,向后移时的二分貌似都没必要写了)
另外,有个 ( ext{julao}) 认为上述证明有问题,但具体她又说不清(这不是在扯淡么),如有不严谨处欢迎指出。
【Code】
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=1e5+5;
int n,s,a[N];LL S[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int judge1(Re i,Re mid){return S[mid]-S[i-1]<=s;}
//judge1()判断序列前半段
inline int judge2(Re i,Re mid){return S[(mid<<1)-i+1]-S[mid]<=s;}
//judge2()判断序列前半段
int main(){
// freopen("b.in","r",stdin);
// freopen("b.out","w",stdout);
in(n),in(s);
for(Re i=1;i<=n;++i)in(a[i]),S[i]=S[i-1]+a[i];
Re p=0;S[n+1]=S[n+2]=1e18;//为防止玄学错误,先把最后面的覆盖一下
while((p+1<<1)<=n&&judge1(1,p+1))++p;//预处理出第一个mid
while(p&&!judge2(1,p))--p;
printf("%d
",(p<<1));
for(Re i=2;i<=n;++i){
// if(p<i-1)p=i-1;//这句可加可不加
while((p+1<<1)-i+1<=n&&judge1(i,p+1))++p;//向后移时注意判断右边界不能超过n
while(p>=i&&!judge2(i,p))--p;//向前移回去,找到最大的合法mid_i
printf("%d
",(p-i+1)<<1);//输出为长度
}
fclose(stdin);
fclose(stdout);
return 0;
}