【学习笔记】OI玄学道—代码坑点
【目录】
- 【逻辑运算符的短路运算】
- 【(cmath) 里的贝塞尔函数】
- 【(scanf) 读入字符】
- 【(cmath) 中的 (pow) 函数】
- 【(vector) 的 (size) 函数】
一:【逻辑运算符的短路运算】
【运算规则】
&& 和 || 属于逻辑运算符。关于 && 和 || 的表达式的运算规则是这样的(用大写字母来表示表达式):
(A) || (B)
只要任意一个表达式为 (true),则整个表达式的运算结果为 (true(1))。
(A) && (B)
仅当所有表达式都为 (true(1)) ,整个表达式的运算结果才为 (true(1)) 。
当任意一个表达式为 (false(0)) ,整个表达式的运算结果则为 (false(0)) 。
【短路运算】
&& 和 || 的短路运算,是指如果在进行前面的表达式的运算过程,通过判断已经明确的知道整个表达式的结果,那么就不会进行后面表达式的运算判断。例如:
(A) || (B) || (C) (....) || (Z)
如果 (A) 的运算结果为 (true(1)) ,则整个表达式的结果为 (true(1)) ,同时不会再对后面的 (B)、(C) 到表达式 (Z) 进行运算判断。
如果 (A) 的运算结果为 (false(0)) ,则根据 (B) 的运算结果继续判断。
(A) && (B) && (C) (....) && (Z)
如果 (A) 的运算结果为 (true(1)) ,则整个表达式的结,如果 (A) 的运算结果为 (false(0)) ,则整个表达式的结果为 (false(0)) ,同时不会再对后面的 (B) 、表达式3到表达式n进行运算判断。如果 (A) 的运算结果为 (true(1)) ,则根据 (B) 的运算结果继续判断。
【小技巧】
把能快速确定整个表达式结果 (true(1)) 或 (false(0)) 的表达式放在前面,这样由于短路运算后面的表达式可能不会被运算到,节省处理器的运算时间。
【坑点】
由于 && 和 || 的表达式存在短路运算现象,在短路之后不会对后面的表达式进行运算,所以含有 && 和 || 的表达式最好不要进行变量的赋值和运算操作,可以先计算好每个表达式的结果,直接拿结果进行 && 和 || 的运算。
在代码编写的时候就要注意这一点,以防由于 && 和 || 的短路运算导致写出来的代码运算结果与预期的不同。
【我心伤悲,莫知我哀】
曾经某个蒟蒻在尝试压行的时候,欣喜O(∩_∩)O~~地发现:
要是把赋值的操作放到判断里面,可以节省大量代码行.
然后(;′⌒`),
......
就没有然后了 (╯ ﹏ ╰)
没错,就是我,而且知道现在才知道当初为什么会错 /(ㄒoㄒ)/~~
好桑心(ㄒ﹏ㄒ)
.......
if(a>1){//b吃c
if(b==c){++ans;continue;};
//食物 天敌 同类
b1=find(b),b2=find(b+n),b3=find(b+2*n);
c1=find(c),c2=find(c+n),c3=find(c+2*n);
if(b2==c3||b3==c1||b3==c3){++ans;continue;};
f[b1]=f[c3],f[c2]=f[b3],f[b2]=f[c1];
}
else{//b,c是同类
//食物 天敌 同类
b1=find(b),b2=find(b+n),b3=find(b+2*n);
c1=find(c),c2=find(c+n),c3=find(c+2*n);
if(b1==c3||b2==c3||c1==b3||c2==b3){++ans;continue;};
f[b3]=f[c3],f[b1]=f[c1],f[b2]=f[c2];
}
if(a>1){
if((b==c)||(b2=find(b+n))==(c3=find(c+2*n))||(b3=find(b+2*n))==(c1=find(c))||b3==c3)++ans;
else f[find(b)]=f[c3],f[find(c+n)]=f[b3],f[b2]=f[c1];
}
else{
if((b1=find(b))==(c3=find(c+2*n))||(b2=find(b+n))==c3||(c1=find(c))==(b3=find(b+2*n))||(c2=find(c+n))==b3)++ans;
else f[b3]=f[c3],f[b1]=f[c1],f[b2]=f[c2];
}
二:【cmath里的贝塞尔函数】
你有使用过 (cmath) 函数库吗?
你有定义全局变量的习惯吗?
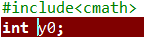
你有定义过 (y0,j0) 变量吗?
当你同时具备以上条件时,恭喜你,踩雷了。

在 (camth) 源代码的 (262) 至 (267) 行有这样一段代码:
_CRTIMP double __cdecl j0 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl j1 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl jn (int, double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl y0 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl y1 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl yn (int, double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
实际上这个叫做 (Bessel) 函数。
所以写代码时应注意不要定义 (j0,j1,jn,y0,y1,yn) 这些变量,但仅限于全局变量,如果是局变量的话,尽情的使用吧。
【参考文献】
三:【scanf读入字符】
由于 (scanf) 的高效,我们通常喜欢用 (scanf) 来读入,然而这东西也会坑人,例如这种情况:
在每行的读入中,由一个字符作为开头。
(cin) 在读入时会跳过空格和换行,(scanf) 只会跳过空格,而不会跳过换行,所以如果直接在每行读入整数之前写 (scanf(“\%c”,&ch)) 的话(.......)
改成 (scanf(“\_\%c”,&ch)) 就可以了(下划线处是一个空格)
四:【cmath中的pow函数】
(camth) 函数库里的 (pow) 函数精度弱的惊人,可能本地自己测数据全对,交上去全 (WA),所以快速幂很重要,不能为了偷懒直接用 (pow),风险较大一般承受不起。
五:【vector的size函数】
(size()) 函数可返回 (vector) 大小,其返回值类型为 (size\_type),应强制转换成 (int) 后再使用,例:
int n=Q.size()-1;
for(int i=0;i<=n;++i);
for(int i=0;i<=(int)(Q.size()-1);++i);
(To) (be) (continued...)

