【题解】PERIOD - Period [POJ1961] [SP263]
在进入这道题之前,我们需要了解 kmp 算法
不知道的童鞋可以去看一下Silent_EAG(一个可爱的女孩纸)的讲解。
关于 kmp 算法中 next 数组的周期性质
引理:
对于某一字符串 (S[1)~(i ]),在它众多的(next[ i ])的“候选项”中,如果存在某一个(next[ i ]),使得: (i) % (( i - next[ i ] ) == 0) ,那么 (S[ 1)~ (( i -next[ i ] ) ]) 可以为 (S[ 1) ~ (i ]) 的循环元而 (i / ( i - next[ i ] )) 即是它的循环次数 (K)。
证明如下:

如图,(next[ i ] = j),由定义得红色部分两个子串完全相同。
那么有(S[ 1)~(j ] = S[ m)~(i ]) (( m = i - next[ i ] ))。

如果我们在两个子串的前面框选一个长度为 m 的小子串(橙色部分)。
可以得到:(S[ 1)~(m ] = S[ m)~(b ])。
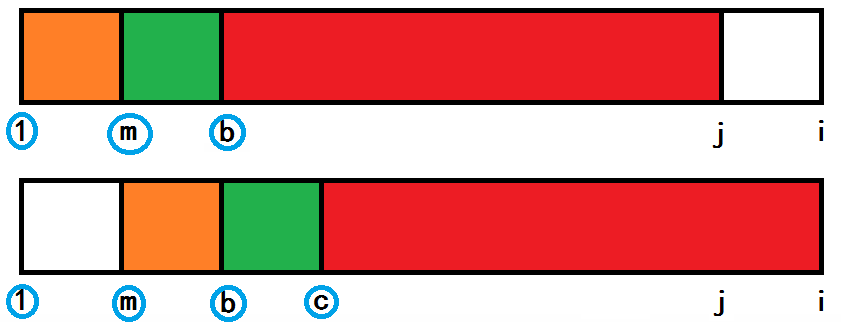
如果在紧挨着之前框选的子串后面再框选一个长度为 m 的小子串(绿色部分),同样的道理,
可以得到:(S[ m)~(b ] = S[ b)~(c ])
又因为:(S[ 1)~(m ] = S[ m)~(b ])
所以:(S[ 1)~(m ] = S[ m)~(b ] = S[ b)~(c ])
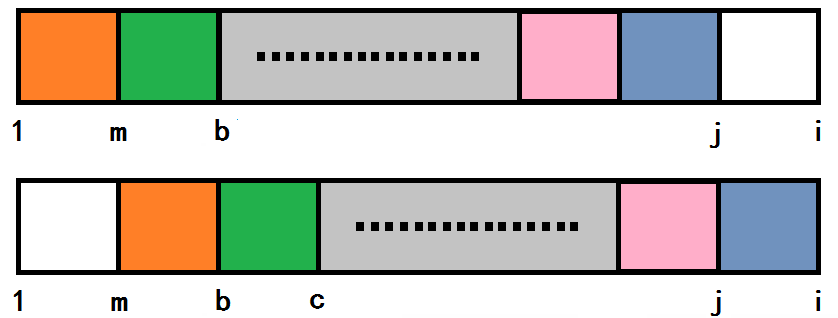
如果一直这样框选下去,无限推进,总会有一个尽头。
当满足 (i) % (m == 0) 时,刚好可以分出 (K) 个这样的小子串,
且形成循环(( K = i / m ))。
因此我们需要从 (1)~(N) 扫一遍,判断如果 (next[ i ])
可以整除 (i) ,即满足 (i) % (( i - next[ ] ) == 0) ,那么就可以
肯定(S[ 1)~ (( i - next[ i ] ) ])是 (S[ 1)~(i ]) 的最小循环元,而
(i / ( i - next[ i ] )) 即是它的最大循环次数 (K) ,直接依次输
出这些 (i)和 (K) 即可。
那么为什么只判断 (next[ i ]) 而不判断 (next[?])呢?
(注:(next[i])和(next[?])表述的意义不同,为方便描
述,这里定义(next[?])为(next[i])的$“候选项”中的某一个)
实际上由这道题可以总结出很多结论:
结论一:
若(i-next[i])可整除(i),则(s[1)~(i])具有长度为(i-next[i])
的循环元,即(s[1)~(i-next[i]])。(前面的一大堆文
字和图片已经给出了这个结论的证明,同时结论一
也是后面推导其他结论的理论基础)
结论二:
若(i-next[?])可整除(i),则(s[1)~(i])具有长度为(i-next[?])
的循环元,即(s[1)~(i-next[?]])。
(用与结论一同样的证明方法可以推导出结论二)
(由此处可知,(i-next[?])想用作循环元要满足的
条件是:(i-next[?])可整除(i))。
结论三:
任意一个循环元的长度必定是最小循环元长度的倍数
结论四:
如果(i-next[i])不可整除(i),(s[1)~(i-next[?]])一定
不能作为(s[1)~(i])的循环元。
关于结论四的证明和扩展:
①.如果(s[1)~(i-next[i]])不能作为(s[1)~(i])循环元,那么
(s[1)~(i-next[?]])也都一定不能作为(s[1)~(i])的循环元。
(即结论四)
②.如果(i-next[i])不可整除(i),(s[1)~(i])一定不存在循环元。
③.如果(i-next[i])不可整除(i),(i-next[?])也都一定不可整除(i)。
④.如果(s[1)~(m])是(s[1)~(i])的循环元,(next[i])一定为(i-m)((i-m)一定为
(next[i]))。(在算法竞赛进阶指南上有这么一句话:如果(s[1)~(m])为(s[1)~(i])的循
环元,(i-m)一定是(next[i])的“候选项”,与此处意义略有不同)
⑤.若(m=i-next[i]),(j=next[?]),(next[j]=j-m)。(无论(m)可否整除(i))
(由④扩展而来)
一些题外话:
关于③的证明,有一个很有趣的想法。
有两个数(a),(c)和一个数的集合(b),且(b)与(a)有一定的关系(限制)。
已知(a)不可整除(c),证明(x(x∈b))不可整除(c)(目前尚未成功)。
虽然表面上看起来并没有什么用,但这种思想把图形匹配转
化为了代数证明。
如果有大佬感兴趣可以思考一下。。。
附:来自某李姓Math大佬。
②③④比较好理解,这个⑤是个什么意思呢?
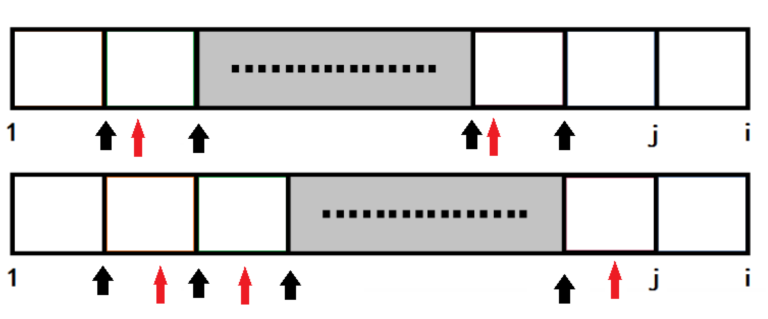
其实不难懂,通俗点说就是(i-next[?])一定是在(m)的倍数处
((m,2m,3m...)),如果有循环,也可以说是(i-next[?])一定在循环
节点上,或者说是一定在我们先前图片中框选的黑色块的边界相
邻处,不可能在某个黑色块的中间(如图红色为不可能的情况)
注意一下这个等式:(i-next[j]=i-j+m)
可以化简为:(next[j]=j-m)
那么可以发现每个(next[?])和(next[next[?]])之间刚好相差m,
只是要由⑤推导①的话,用化简前的样子似乎会更好懂一些。
假如④⑤得证,那么它们和①有什么关系呢?
如果(i-next[?])一定是在(m)的倍数处((m=i-next[i])),
因为当(m)不可整除(i)时,(m)的倍数也不可整除(i),
所以(i-next[?])均不满足作为(s[1)~(i])循环元的条件(前面已
提到过“条件”具体指什么)。
因此,⑤(→)①得证。
如何证明④或者⑤?
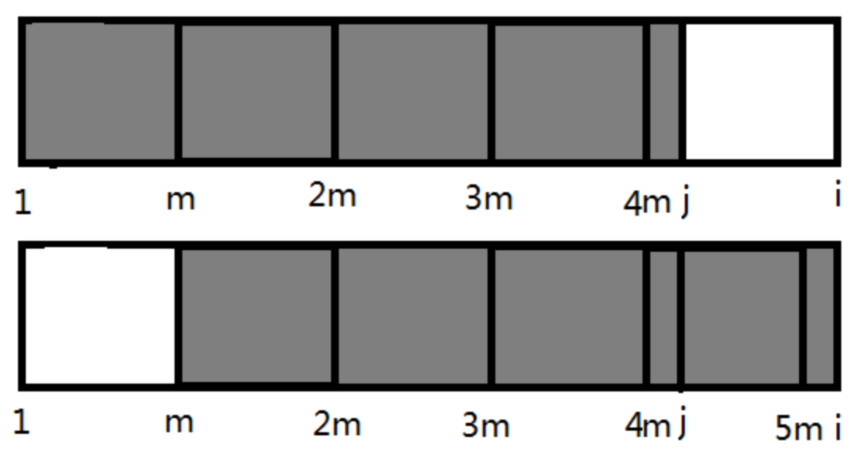
如图,(j=next[i]),(m=i-next[i])
先按照与之前相同的方法先将(s[1)~(i])划分成(K)个黑色块
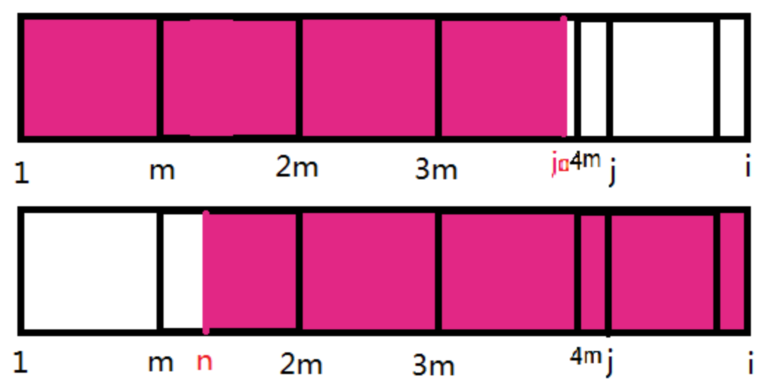
(j0=next[j]),(n=i-next[j]),假设n不在m的倍数处,如图红色。
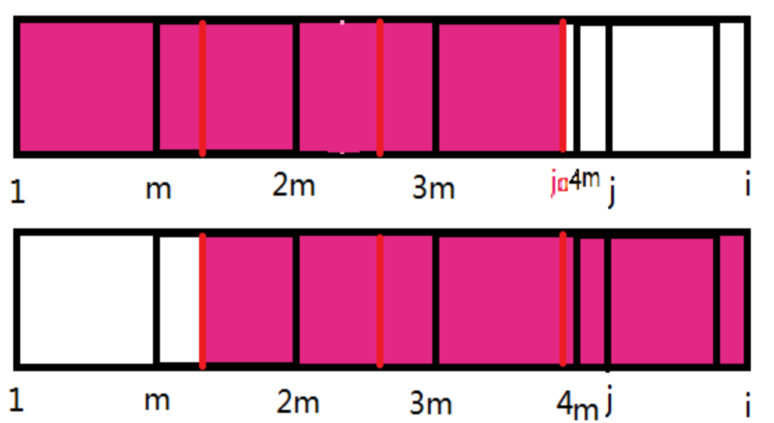
同样的,框选出红色块。
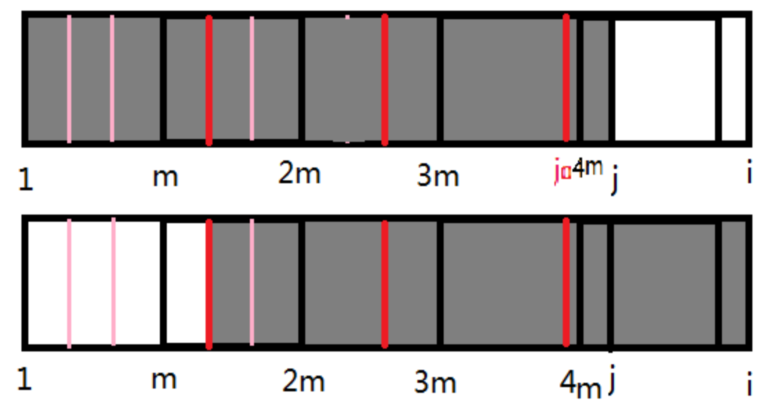
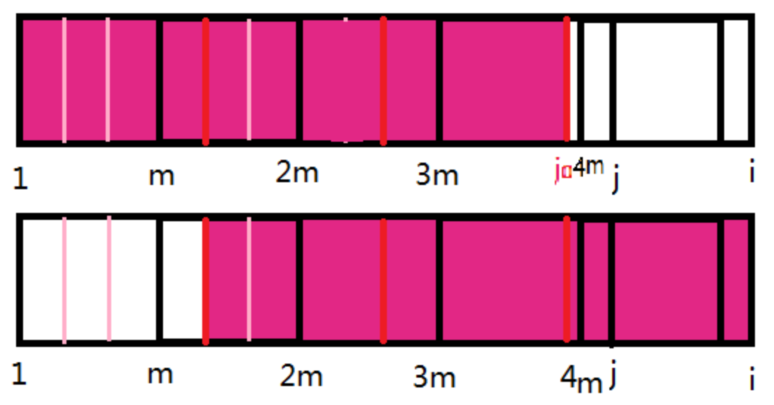
然后再作一些辅助线。接下来就开始推理。
设(v=j-j0)。
先看左边:(s[1)~(1+v]=s[m)~(m+v]),(s[1+v)~(1+2v]=s[m+v)~$m+2v] $
再看右边: (s[1)~(1+v]=s[m+v)~(m+2v])
综合可得:(s[1)~(1+v]=s[m)~(m+v]=s[m+v)~(m+2v]=s[1+v)~(1+2v])
无限的推进,再推进,辅助线划分出的长度为v的区域全部相等,直至边界。而此时的边界出现了两种情况:
⑴v可整除i。
此时刚好将(s[1)~(i])分成了若干个完全相同的长度为(v)的小块,明显形成了循环元(s[1)~(v]),那么(next[i])至少应为(i-v),这与之前的(next[i]=j)相矛盾。
⑵v不可整除i。
观察下列图片,你发现了什么?
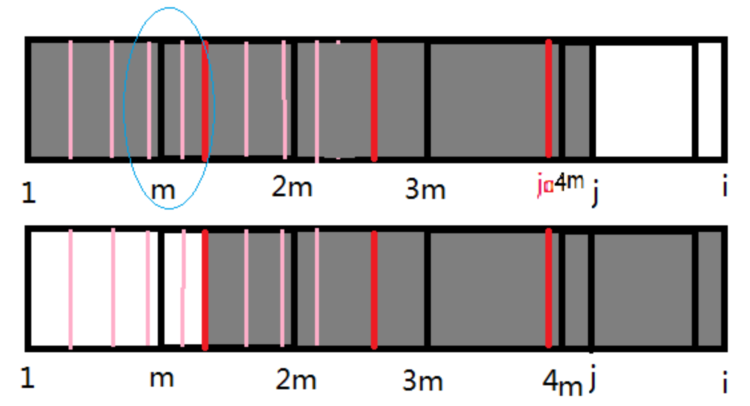
将蓝圈处放大,发现了一种交叉相等的情况(如图绿色处)。
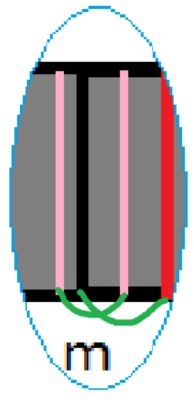
再把它压扁,并取几个新的名字(1',m',j',i')。此时它变得和初始
的情况一模一样,于是经过相同的操作后,再一次使出了无限
推进,假如每次的(v')都不可整除(m'),那么就一路推了边界:(v'=1)。
(1)可以整除任何数,于是(s[1)~(i])形成了长度为(1)的循环元,矛盾。
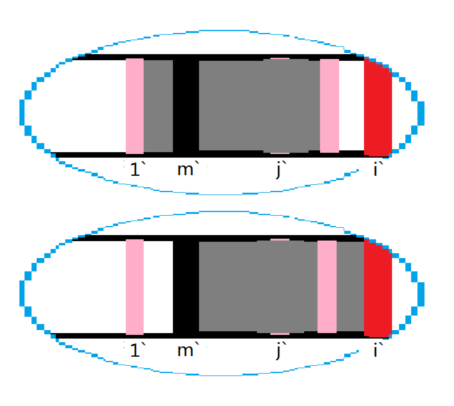
当n不在m的倍数处时,一定会出现矛盾,所以假设不成立。
因此④得证。同理⑤也得证。
完结附代码:
#include<cstdio>
int t,i,j,n,nex[1000005];char a[1000005];
int main(){
while(scanf("%d",&n),n){
scanf("%s",a+1);
printf("Test case #%d
",++t);
for(i=2,j=0;i<=n;i++){//最基本的 next[] 数组求法
while(j&&a[i]!=a[j+1])j=nex[j];
if(a[i]==a[j+1])j++;nex[i]=j;
}
for(i=2;i<=n;i++)//由于1~1只有一个字母,只能是它本身构成长度为1的循环,所以从2开始枚举
if(i%(i-nex[i])==0&&nex[i])//判断时还要注意nex[i]是否为0
printf("%d %d
",i,i/(i-nex[i]));
//如果i含有长度大于1的最小循环元,输出i的长度(即i)以及最大循环次数K(即i-nex[i])
printf("
");//记得输出一个空行
}
}
写了这么多证明,结果最后代码简单得不要不要的。。。。。