参考了:https://blog.csdn.net/u011885865/article/details/42032229
需要的基础:学过《线性代数》,知道行列式值的求法
基本公式:对于如下的行列式:

其值为:
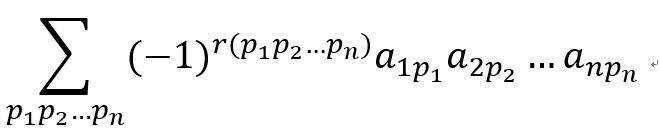
相信大家都懂这个公式的具体含义,我就不解释了,不懂的同学百度一下行列式
分析一个这个公式该如何实现:
假定现有有一个3*3的行列式,则其计算公式为:
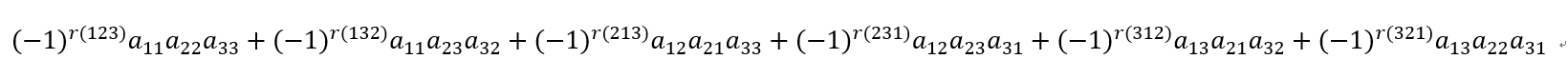
观察这个式子,可以发现其有一个核心,那就是生成一个全排列。本例中是一个3*3矩阵,因此需要生成123的全排列,共有六个:123、132、213、231、321、312。
然后就是要计算,生成的排列的逆序数,即
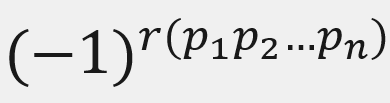
总结起来可分为如下几步:
1、求出给定n阶矩阵的全排列,我用vector<int>存储一个全排列(即上例中6个全排列中的某一个),用vector<vector<int> >存储所有的全排列(即上例中的六个全排列)。
2、计算排列的逆序数。
3、分别以1,2...n为row值,从vector<int>中依次提取的值为col值,组成行列式中元素的下标,然后相乘
4、求和。
算法实现:
1、求全排的算法如下,不懂该算法的可以移步:https://www.cnblogs.com/XiaoXiaoShuai-/p/10383535.html
//交换元素
void swap(vector<int>& vec, int i, int j)
{
int temp = vec[i];
vec[i] = vec[j];
vec[j] = temp;
}
//第一个参数表示初始的数列,在上例中,该vec中的元素为1,2,3
//第二个参数表示最终得到的全排列集合
void Perm(vector<int>& vec, vector<vector<int> >& vec_seq, int current_index = 0)
{
if (current_index == ((int)vec.size() - 1))
{
vec_seq.push_back(vec);
}
else
{
for (int i = current_index; i < (int)vec.size(); i++)
{
swap(vec, i, current_index);
Perm(vec, vec_seq, current_index + 1);
swap(vec, i, current_index);
}
}
}
当然,还得有一个生成初始数列的函数
//根据n生成一个初始vector
vector<int> inivec(int n)
{
vector<int> vec;
for (int i = 0; i < n; i++)
vec.push_back(i);
return vec;
}
第二步:求出全排列的逆序数,判断逆序数的奇偶
//得出排列的逆排序数,并根据奇偶判读正负
bool Iseven(int num)
{
//用位与运算来判断奇偶(最快的判断奇偶的方法)
return ((num & 1) == 0);
}
//是否幂为正
bool PowerIsPosition(vector<int>& vec)
{
//count即为逆序数,初始化为0
int count = 0;
for (int i = 0; i < (int)vec.size(); i++)
{
for (int j = i + 1; j < (int)vec.size(); j++)
{
if (vec[i] > vec[j])
{
count += 1;
}
}
}
return (Iseven(count));
}
第三步和第四步:
//计算结果
//第一个参数表示输入的行列式
//第二个参数表示该行列式的阶数,在本例中n = 3,即一个3*3的行列式
int calculate(int** array, int n)
{
vector<vector<int> > vec_que;
vector<int> vec = inivec(n);
vector<int> vec_elem;
Perm(vec, vec_que);
//最终结果,初始化为0
int result = 0;
//依次为vec_que中取出行列式
for (int i = 0; i < (int)vec_que.size();i++)
{
vec_elem = vec_que[i];
//mi即为前面(-1)的n次幂,最后结果为-1或者1
int mi = PowerIsPosition(vec_elem) ? 1 : (-1);
int temp = mi;
//row号初始化为0之后依次加1
int row = 0;
//col号依次从vec_elem中取出
for (int j = 0; j < (int)vec_elem.size();j++)
{
int col = vec_elem[j];
temp *= array[row++][col];
}
result += temp;
}
return result;
}
检验一下:
int main()
{
int** array = new int*[3];
for (int i = 0; i < 3; i++)
{
array[i] = new int[3];
}
array[0][0] = 2;
array[0][1] = -4;
array[0][2] = 1;
array[1][0] = 1;
array[1][1] = -5;
array[1][2] = 3;
array[2][0] = 1;
array[2][1] = -1;
array[2][2] = 1;
int result = calculate(array, 3);
return 0;
}
计算的result = -8,结果正确