图的存储方式：邻接矩阵和邻接表【基础】

注：本文已迁移至CSDN，后续的更新也会在CSDN。

http://blog.csdn.net/houchaoqun_xmu/article/details/53813630

http://blog.csdn.net/houchaoqun_xmu

【原】本文主要简单介绍了“数据结构”中，图的存储方式，包括邻接矩阵的存储方式和邻接表的存储方式，并使用C++进一步实现。

-- 说明：本博文属于基础篇，适合于初学或者尚未学且对数据结构感兴趣的同学，核心内容如下：

　　1. 图的存储结构理论简介，以及创建图的算法；

　　2. 无向邻接矩阵的应用，主要介绍了通过文件流读取城市路径（旅行商问题）的相关数据，将值赋给图的数据结构相关的成员；

　　3. 关于旅行商问题的数据说明与处理；

-- 此外，在本文的基础上，后续还会有6篇左右的文章基于图的存储结构，解决TSP旅行商问题，分别包括如下标题：

-------------------------------------------------------------------------------------------------
（1）TSP_旅行商问题- 蛮力法( 深度遍历优先算法DFS )
（2）TSP_旅行商问题- 动态规划
（3）TSP_旅行商问题- 模拟退火算法
（4）TSP_旅行商问题- 遗传算法
（5）TSP_旅行商问题- 粒子群算法

-------------------------------------------------------------------------------------------------

一、图的存储结构

1. 邻接矩阵表示法 - 以无向图为例：

　　1）邻接矩阵简介

　　　　-- 逻辑结构分为两部分：Vexs[]（存储顶点）和Arcs[][]（邻接矩阵）集合。因此，用一个一维数组存放图中所有顶点数据；用一个二维数组存放顶点间关系（边或弧）的数据，这个二维数组称为邻接矩阵。

　　　　-- 邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵，此处以无向图为例。

　　2）无向图邻接矩阵的特点：

　　　　-- 对无向图而言，邻接矩阵一定是对称的，而且主对角线一定为零（在此仅讨论无向简单图），副对角线不一定为0，有向图则不一定如此；

　　　　-- 无向图邻接矩阵是一个对称矩阵；

　　　　-- 顶点Vi的度等于第i行非零元个数，或第i列非零元个数；（有向图没有此特点）

　　　　

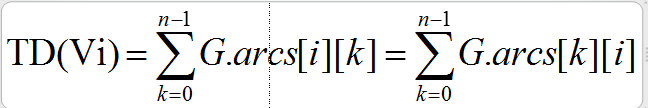
　　　　-- 矩阵非零元总数等于边数的2倍；

　　　　-- 用邻接矩阵表示图，很容易确定图中任意两个顶点是否有边相连；

 　　3）完整的数据结构表示如下：

/* 1. 图 - 邻接矩阵表示法 */
/* ---------------------------------------------------------------- */
/* 较完善的数据结构 */
#define VRType int
#define InfoType int
#define VertexType char
#define max_n 20
typedef enum{DG, DN, AG, AN} GraphKind;

//  弧结点与矩阵的类型
typedef struct { 
    VRType    adj;          //VRType为弧的类型。图--0,1;网--权值
    InfoType  *Info;        //与弧相关的信息的指针,可省略
}ArcCell, AdjMatrix[max_n][max_n];

//  图的类型
typedef struct{        
    VertexType vexs[max_n];     // 顶点向量
    AdjMatrix  arcs;            // 邻接矩阵
    int        vexnum, arcnum;  // 顶点数，边数
    GraphKind  kind;            // 图类型
}MGraph;     
 
/* ---------------------------------------------------------------- */

　　4）【具体问题具体分析】根据”TSP“旅行商问题的需求，将该无向图的邻接矩阵简化如下：

/* 简化的数据结构 */

#define max_vexNum 26    // 最大城市个数
#define MAX_PATH_LENGTH 9999999
typedef struct{
    int vex_num, arc_num;                   // 顶点数 边数
    char vexs[max_vexNum];                  // 顶点向量
    double arcs[max_vexNum][max_vexNum];    // 邻接矩阵
}Graph;

　　5）基于邻接矩阵创建图 - CreateGraph()

1. 输入图的类型Kind，0--有向图，2--无向图;
2. 输入顶点数G.vexnum和边数G.arcnum;
3. 输入n个顶点，填入顶点数组G.vexs；
4. 输入边的偶对(vi,vj)或<vi,vj>, 填写邻接矩阵G.arcs

　　6）无向图的邻接矩阵图例

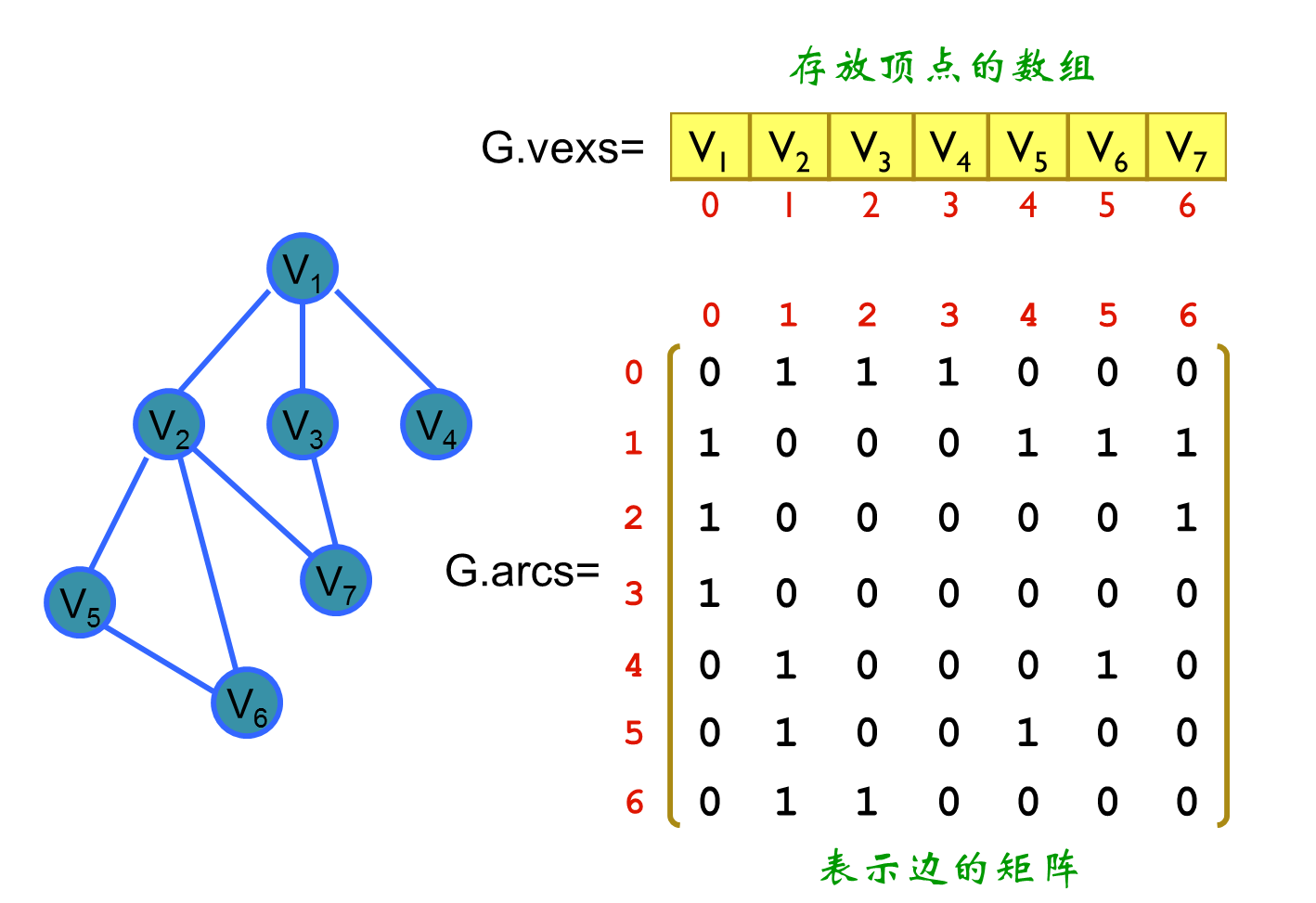
2. 邻接表表示法 - 将每个顶点的邻接点串成一个单链表

 　　1）邻接表的数据结构

#define  max_n   20            　　　　//最大顶点数
typedef struct ArcNode{        　　　　//边结点
     int            adjvex;    　　　　//邻接点的下标
     struct ArcNode    *nextarc;     //后继链指针
}ArcNode;

typedef struct VNode{        　　　　//顶点结点
     VertexType       data;        //顶点数据           
     ArcNode           *firstarc;  //边链头指针
}VNode, AdjList[max_n];       

typedef struct{
     AdjList        vertices;       //邻接表
     int        vexnum,arcnum;     //顶点数和边数
     GraphType    kind；        　　//图种类标志
}ALGraph;

　　2）无向图的邻接表 - 实例：

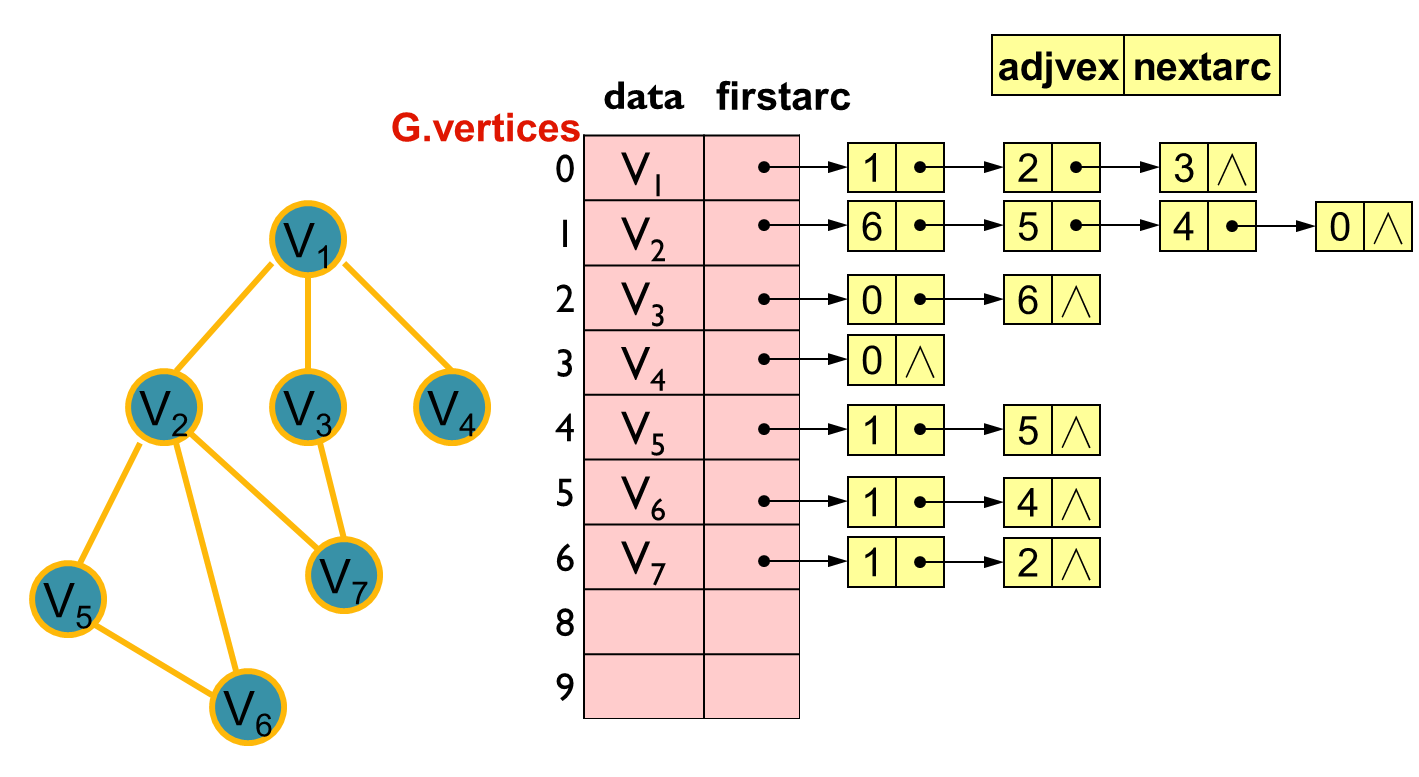
　　3）基于邻接表创建图 - CreateGraph()

1. 输入图的类型Kind，0--有向图，2--无向图;
2. 输入顶点数G.vexnum和边数G.arcnum;
3. 输入n个顶点，填入顶点数组G.vextices；
4. 输入边的偶对(vi,vj)或<vi,vj>, 用头插法生成边链

二、C++实现图的邻接矩阵表示法

1. 数据结构

/* 简化的数据结构 */

#define max_vexNum 26    // 最大城市个数
#define MAX_PATH_LENGTH 9999999
typedef struct{
    int vex_num, arc_num;                  // 顶点数 边数
    char vexs[max_vexNum];                 // 顶点向量
    double arcs[max_vexNum][max_vexNum];   // 邻接矩阵
}Graph;

2. 文件读取的方式，本程序采用文件流的方式进行数据的读写，相关代码如下：

#include <fstream>

ifstream read_in;
read_in.open("L:\Coding\图的常见操作\图的常见操作\city_10.txt");
if (!read_in.is_open())
{
    cout<<"文件读取失败."<<endl;
    return;
}

3. TSP（旅行商问题）的实验数据：文件名（ city_10.txt ）

10
A B C D E F G H I J 
0 2538.94 2873.8 2575.27 2318.1 2158.71 2216.58 3174.04 3371.13 3540.24 
2538.94 0 1073.54 111.288 266.835 395.032 410.118 637.942 853.554 1055 
2873.8 1073.54 0 964.495 988.636 1094.32 1382.73 1240.15 1460.25 1687 
2575.27 111.288 964.495 0 262.053 416.707 503.563 624.725 854.916 1068.42 
2318.1 266.835 988.636 262.053 0 163.355 395.14 885 1110.86 1318.19 
2158.71 395.032 1094.32 416.707 163.355 0 338.634 1030.34 1248.58 1447.69 
2216.58 410.118 1382.73 503.563 395.14 338.634 0 984.068 1160.26 1323.7 
3174.04 637.942 1240.15 624.725 885 1030.34 984.068 0 243.417 473.768 
3371.13 853.554 1460.25 854.916 1110.86 1248.58 1160.26 243.417 0 232.112 
3540.24 1055 1687 1068.42 1318.19 1447.69 1323.7 473.768 232.112 0 

4. 创建TSP城市的邻接矩阵

void CreateGraph(Graph &G){
    ifstream read_in;
    read_in.open("L:\Coding\图的常见操作\图的常见操作\city_10.txt");
    if (!read_in.is_open())
    {
        cout<<"文件读取失败."<<endl;
        return;
    }
    
    read_in >> G.vex_num;
    // read_in >> G.arc_num;
    G.arc_num = 0;
    for (int i = 0;i < G.vex_num; i++)
    {
        read_in >> G.vexs[i];
    }
    G.vexs[G.vex_num] = '';    // char的结束符.

    for (int i = 0; i < G.vex_num;i++)
    {
        for (int j = 0; j < G.vex_num; j++)
        {
            read_in >> G.arcs[i][j];

            // calculate the arc_num
            if (G.arcs[i][j] > 0)
            {
                G.arc_num++;
            }
        }
    }

    // display
    cout<<"无向图创建完毕，相关信息如下："<<endl;
    cout<<"【顶点数】 G.vex_num = "<<G.vex_num<<endl;
    cout<<"【边数】 G.arc_num = "<<G.arc_num<<endl;
    cout<<"【顶点向量】 vexs[max_vexNum] = ";
    for (int i = 0; i < G.vex_num; i++)
    {
        cout<<G.vexs[i]<<" ";
    }
    cout<<endl<<"【邻接矩阵】 arcs[max_vexNum][max_vexNum] 如下："<<endl;
    for (int i = 0; i < G.vex_num;i++)
    {
        for (int j = 0; j < G.vex_num; j++)
        {
            cout << std::right<<setw(10) << G.arcs[i][j]<<" ";
        }
        cout<<endl;
    }
}

5. 实验结果

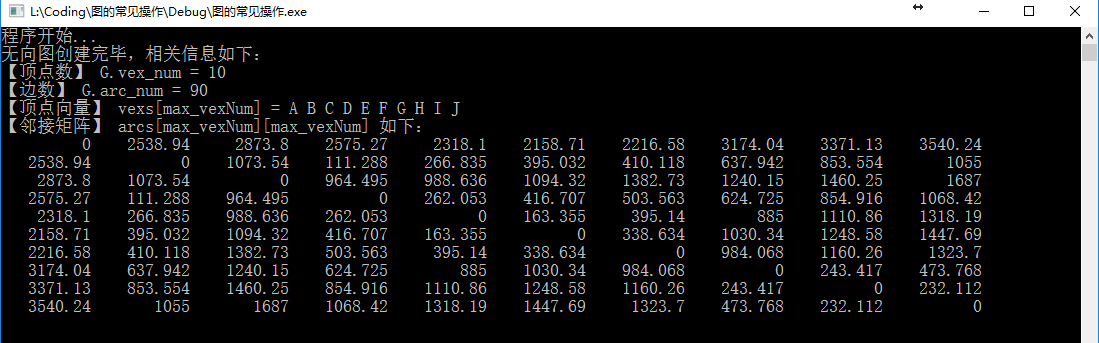
6. 旅行商问题数据的说明与处理

　　1）旅行商问题的数据说明：

　　　  -- 目前网上有很多我国城市相关的数据，以坐标点的方式表示，而本程序以及后续的程序都是以邻接矩阵的方式体现，所以现在需要将数据进行转换。

　　　  -- 【城市数据】  参考网址：http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/

　　　  -- 【TSP最优解】参考网址：http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/STSP.html

 　　2）转换程序如下：

// 城市数据格式转化

#define MAX_CITYNUM 150
void CityDataTranslate(){
    ifstream read_in;
    read_in.open("L:\Coding\TSP_SA模拟退火算法\TSP_SA模拟退火算法\ch150.txt");        // 待转换数据，数据可从上述链接【城市数据】下载
    if (!read_in.is_open())
    {
        cout<<"文件读取失败."<<endl;
        return;
    }

    ofstream fout("L:\Coding\TSP_SA模拟退火算法\TSP_SA模拟退火算法\city_150.txt");        // 转换后的数据存入文档 city_150.txt

    double city_table[MAX_CITYNUM][MAX_CITYNUM];
    int city_No[MAX_CITYNUM];
    double city_x[MAX_CITYNUM];
    double city_y[MAX_CITYNUM];

    int vex_num;
    read_in >> vex_num;
    fout << vex_num << endl;

    for (int i = 0; i < vex_num; i++)
    {
        read_in >> city_No[i] >> city_x[i] >> city_y[i];

        fout << i + 1 <<" ";
    }
    fout<<endl;

    for (int i = 0; i < vex_num; i++)
    {
        city_table[i][i] = 0;
        for (int j = 0; j < vex_num; j++)
        {
            double temp = (city_x[i] - city_x[j])*(city_x[i] - city_x[j]) + (city_y[i] - city_y[j])*(city_y[i] - city_y[j]);
            city_table[i][j] = sqrt(temp);
            fout << city_table[i][j]<<" ";
        }
        fout<<endl;
    }
}

 -------------------------------------------------------------

【注】博文由本文经过实践进一步整理，如有问题，还望指出，本人会及时纠正！谢谢^^

--------------------------------------------------------------