由于林荫要准备CSP-S(拿不到的话就可能要去郸城一高了),因此开始复习以前写过的所有算法。
在此先致敬一下Robert Tarjan,这位老先生现在仍在为人类做贡献。
Tarjan求LCA算法属于离线算法,要求事先得知所要求解的点对。
算法由一个DFS组成,伪代码大意就是:
DFS(x)
{
1.对于该点打上访问标记
2.将该点的父节点置为自己
3.访问这个点的每一个子节点,对每个子节点进行DFS
4.将子节点的父亲置为自己
5.对每一个关于这个节点的询问进行遍历
6.如果这个点的对应节点已经被访问,那么答案就是对应节点的最终祖先,否则跳过。
}
这样的话就是一个简单的DFS就可以结束了。
代码放一下:
int dfs(int x){//把整棵树的一部分看作以节点x为根节点的小树 father[x]=x;//由于节点x被看作是根节点,所以把x的father设为它自己 visit[x]=1;//标记为已被搜索过 for(int k=head[x];k;k=edge[k].next)//遍历所有与x相连的节点 if(!visit[edge[k].to]){//若未被搜索 dfs(edge[k].to);//以该节点为根节点搞小树 father[edge[k].to]=x;//把x的孩子节点的father重新设为x } for(int k=qhead[x];k;k=qedge[k].next)//搜索包含节点x的所有询问 if(visit[qedge[k].to]){//如果另一节点已被搜索过 qedge[k].lca=find(qedge[k].to);//把另一节点的祖先设为这两个节点的最近公共祖先 if(k%2)//由于将每一组查询变为两组,所以2n-1和2n的结果是一样的 qedge[k+1].lca=qedge[k].lca; else qedge[k-1].lca=qedge[k].lca; } }
很简单对吧!
正确性证明:
先放张图:鸣谢林荫的好队友兼摄影师一只jinx大佬哈。
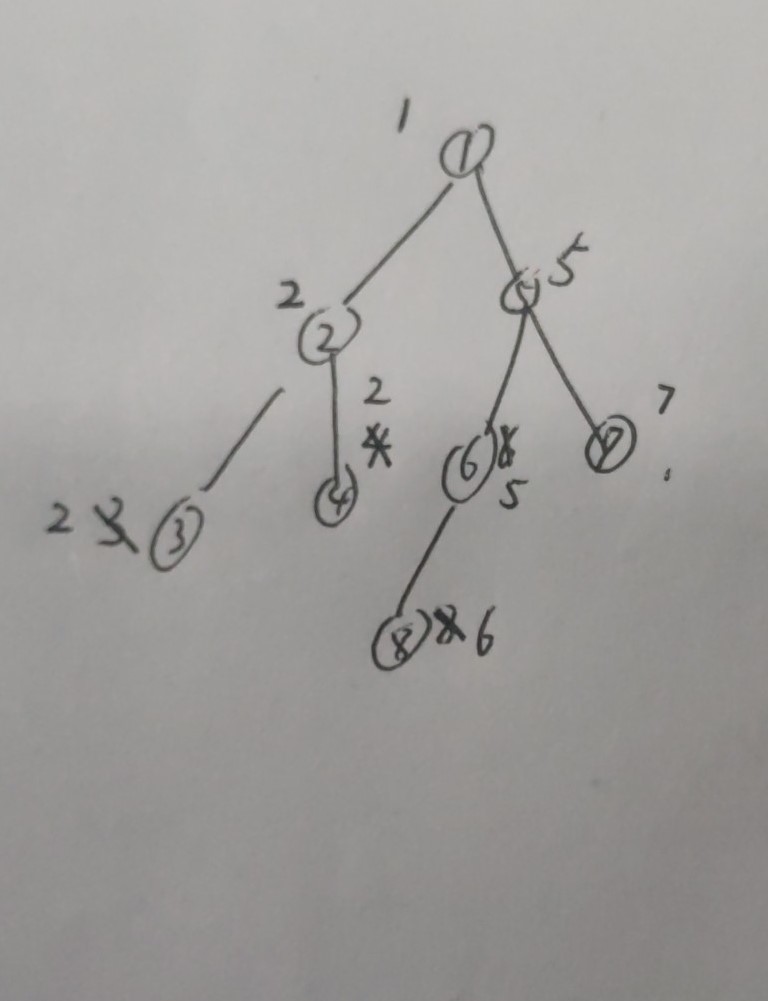
圈内的编号是点的序号,点上被划掉的数字是这个点的父亲曾经所存的值,没被划掉的是最后一次存下的父亲的值。
图中少修改了一次值,2节点上面的2应当被划掉修改成1
仔细看图可以确定现在DFS进行到了哪里?
仔细看图,看图,看图!!!
没错,是走到了7号节点,也就是说,当前最内层DFS的x值是7.
我们很容易的可以知道,现在每个节点都已经被标记了。假定有询问点对1——7,3——7,6——7,5——7。
我们一个一个看,对于1节点,因为已经被访问过,LCA即为1的父亲。对于3节点,LCA=Lastfa[3]=Lastfa[2]=Lastfa[1]=1.
对于6——7,LCA=Lastfa[6]=5,对于5——7同理。
因为当一个点的对应点已经被访问过之后,代表两点一定在同一条链,或者两点不在同一颗子树上。因为每一次对于某个点的子节点全部访问完毕后,子节点的父亲都会被置为这个点,否则不变。也就是说,对应点的父节点的Lastfa一定是遍历进入这个点之前所访问过的深度最小的点。 大家可以将其理解为爬山一样,先在山脚找到点对中第一个点,然后向上爬,爬到一个可以到达第二个点的地方。因为DFS是从上向下找,到最底部之后再开始一点一点向上爬,找到最近的岔路口之后就向岔路口走去,也就是说我们在爬山过程中找到的一定是LCA。
最后放个代码吧。
#include<iostream> #include<cstdio> #define N 1000001 struct hehe{ int next; int to; int lca; }; hehe edge[N];//树的链表 hehe qedge[N];//需要查询LCA的两节点的链表 int n,m,p,x,y; int num_edge,num_qedge,head[N],qhead[N]; int father[N]; int visit[N];//判断是否被找过 void add_edge(int from,int to){//建立树的链表 edge[++num_edge].next=head[from]; edge[num_edge].to=to; head[from]=num_edge; } void add_qedge(int from,int to){//建立需要查询LCA的两节点的链表 qedge[++num_qedge].next=qhead[from]; qedge[num_qedge].to=to; qhead[from]=num_qedge; } int find(int z){//找爹函数 if(father[z]!=z) father[z]=find(father[z]); return father[z]; } int dfs(int x){//把整棵树的一部分看作以节点x为根节点的小树 father[x]=x;//由于节点x被看作是根节点,所以把x的father设为它自己 visit[x]=1;//标记为已被搜索过 for(int k=head[x];k;k=edge[k].next)//遍历所有与x相连的节点 if(!visit[edge[k].to]){//若未被搜索 dfs(edge[k].to);//以该节点为根节点搞小树 father[edge[k].to]=x;//把x的孩子节点的father重新设为x } for(int k=qhead[x];k;k=qedge[k].next)//搜索包含节点x的所有询问 if(visit[qedge[k].to]){//如果另一节点已被搜索过 qedge[k].lca=find(qedge[k].to);//把另一节点的祖先设为这两个节点的最近公共祖先 if(k%2)//由于将每一组查询变为两组,所以2n-1和2n的结果是一样的 qedge[k+1].lca=qedge[k].lca; else qedge[k-1].lca=qedge[k].lca; } } int main(){ scanf("%d%d%d",&n,&m,&p);//输入节点数,查询数和根节点 for(int i=1;i<n;++i){ scanf("%d%d",&x,&y);//输入每条边 add_edge(x,y); add_edge(y,x); } for(int i=1;i<=m;++i){ scanf("%d%d",&x,&y);//输入每次查询,考虑(u,v)时若查找到u但v未被查找,所以将(u,v)(v,u)全部记录 add_qedge(x,y); add_qedge(y,x); } dfs(p);//进入以p为根节点的树的深搜 for(int i=1;i<=m;i++) printf("%d ",qedge[i*2].lca);//两者结果一样,只输出一组即可 return 0; }
完结撒花!!!