【Leetcode】402.移掉K位数字（单调栈）

单调栈的应用

402. 移掉K位数字

316. 去除重复字母

321. 拼接最大数

1.题目链接

402. 移掉K位数字

题目描述

解题思路

一招吃遍力扣四道题，妈妈再也不用担心我被套路啦～

贪心+单调栈

本题采用贪心思路+单调栈

• 如果字符串按照数字大小升序排列，只需要删除最后K个字符即可；
• 如果非升序排列，需要从前到后遍历，删除字符串中每个逆序排列的字符。由于是从前到后遍历，所以先删除的一定是高位的数字，可以保证删除后得到的最终数字最小。
• 举例来说：如果字符串num = "123456789", k = 3，我们只需要删除最后3个数字，得到"123456"。如果字符串num = "1432219", k = 3，需要从前到后遍历查找逆序数字，进行删除，第一个逆序数字为'4'，第二个逆序数字为'3'，第三个逆序数字为第二个'2'，最后得到"1219"。

所以可以采用栈实现，每次遍历，判断如果栈非空，且当前数字大于栈顶数字，且k还有剩余（不为0），将栈顶数字出栈。最后将当前数字入栈。

如果遍历完成后，k仍有剩余，则依次将栈顶数字出栈。最后栈中保存的数字即为所求。按照从栈底到栈顶输出即可。

注意：特判场景，如果最后所有数字均出栈，即栈为空，需要返回"0"。

贪心+用String实现单调栈

对时间复杂度进行优化

AC代码

贪心+单调栈

class Solution {
    public String removeKdigits(String num, int k) {
        if(k == 0) return num;
        if(k == num.length()) return "0";
        Stack<Character> s = new Stack<>();
        int index = 0;
        while(index < num.length()){
            while(k > 0 && s.size() > 0 && num.charAt(index) < s.peek()){
                s.pop();
                k--;
            }
            //前导0情况的处理
            if(s.size() == 0 && num.charAt(index) == '0') {
                index++;
                continue;
            }
            s.push(num.charAt(index));
            index++;
        }
        String ans = "";
        while(k > 0){
            s.pop();
            k--;
        }
        if(s.size() == 0) return "0";
        while(!s.isEmpty()) ans += s.pop();
        return new StringBuffer(ans).reverse().toString();
    }
}

2.题目链接

316. 去除重复字母

题目描述

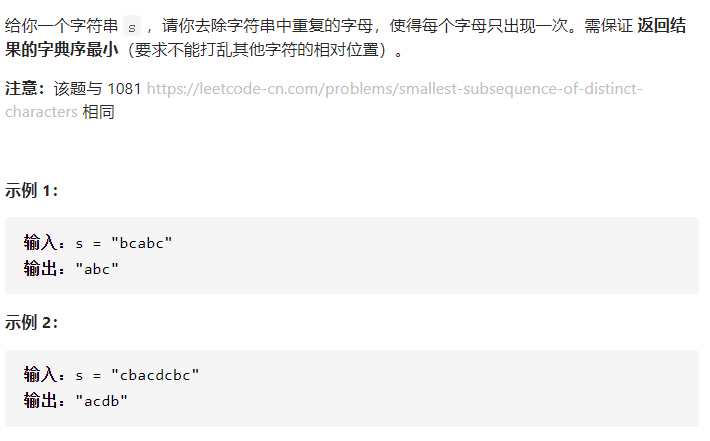
解题思路

https://leetcode-cn.com/problems/remove-duplicate-letters/solution/you-qian-ru-shen-dan-diao-zhan-si-lu-qu-chu-zhong-/

这篇解析真的写太棒了

AC代码

class Solution {
    public String removeDuplicateLetters(String s) {
        char strToChar[] = s.toCharArray();
        int[] countChar = new int[100];
        StringBuffer tack = new StringBuffer();
        boolean[] existChar = new boolean[100];
        for(int i = 0; i < strToChar.length; i++){
            countChar[strToChar[i]-'0']++;
        } 
        Stack<Character> st = new Stack<>();
        for(int i = 0; i < strToChar.length; i++){
            countChar[strToChar[i]-'0']--;
            //此行代码很关键字，如果栈中已经存在该元素了，则直接跳过无需考虑，刚开始自己就是一直卡在这个条件判断上，浪费了很多时间。
            if(existChar[strToChar[i]-'0'] == true) continue;
            while(st.size() > 0 && strToChar[i] < st.peek() && countChar[st.peek()-'0'] > 0){
                existChar[st.pop()-'0'] = false;
            }
            st.push(strToChar[i]);
            existChar[strToChar[i]-'0'] = true;
        }
        StringBuffer ans = new StringBuffer();
        while(!st.isEmpty()) ans.append(st.pop());
        return ans.reverse().toString();
    }
}

利用Stringbuffer替代栈的功能（实现单调栈）

//利用Stringbuffer替代栈的功能
class Solution {
    public String removeDuplicateLetters(String s) {
        char strToChar[] = s.toCharArray();
        int[] countChar = new int[100];
        boolean[] existChar = new boolean[100];
        StringBuffer tack = new StringBuffer();
        for(int i = 0; i < strToChar.length; i++){
            countChar[strToChar[i]-'0']++;
        } 
        for(int i = 0; i < strToChar.length; i++){
            countChar[strToChar[i]-'0']--;
            if(existChar[strToChar[i]-'0']) continue;
            while(tack.length() > 0 && strToChar[i] < tack.charAt(tack.length()-1) && countChar[tack.charAt(tack.length()-1)-'0'] > 0){
                existChar[tack.charAt(tack.length()-1)-'0']=false;
                tack.deleteCharAt(tack.length()-1);
            }        
            tack.append(strToChar[i]);  
            existChar[strToChar[i]-'0'] = true;   
        }
        return tack.toString();
    }
}

3.题目链接

321. 拼接最大数

题目描述

解题思路

将数字数组转换为字符串更加方便处理。然后利用单调栈处理

和第一道题类似，只不过这一次是两个数组，而不是一个，并且是求最大数。

最大最小是无关紧要的，关键在于是两个数组，并且要求从两个数组选取的元素个数加起来一共是 k。

然而在一个数组中取 k 个数字，并保持其最小（或者最大），我们已经会了（利用单调栈）。但是如果问题扩展到两个，会有什么变化呢？

实际上，问题本质并没有发生变化。 假设我们从 nums1 中取了 k1 个，从 num2 中取了 k2 个，其中 k1 + k2 = k。而 k1 和 k2 这 两个子问题我们是会解决的。由于这两个子问题是相互独立的，因此我们只需要分别求解，然后将结果合并即可。

假如 k1 和 k2 个数字，已经取出来了。那么剩下要做的就是将这个长度分别为 k1 和 k2 的数字，合并成一个长度为 k 的数组合并成一个最大的数组。

以题目的 nums1 = [3, 4, 6, 5] nums2 = [9, 1, 2, 5, 8, 3] k = 5 为例。 假如我们从 num1 中取出 1 个数字，那么就要从 nums2 中取出 4 个数字。

运用第一题的方法，我们计算出应该取 nums1 的 [6]，并取 nums2 的 [9,5,8,3]。 如何将 [6] 和 [9,5,8,3]，使得数字尽可能大，并且保持相对位置不变呢？

实际上这个过程有点类似归并排序中的治，而上面我们分别计算 num1 和 num2 的最大数的过程类似归并排序中的分。

AC代码

class Solution {
	//利用单调栈求出nums数组中个数为k的最大数
    String pickMax(int[] nums,int k){
        int tot = nums.length;
        Stack<Integer> st = new Stack<>();
        StringBuffer ans = new StringBuffer();
        if(tot == k){
            for(int i : nums) ans.append(i);
            return ans.toString();
        }
        else if(k != 0){
            for(int i = 0; i < nums.length; i++){
                while(st.size() != 0 && nums[i] > st.peek()){
                    if(st.size() + tot > k) st.pop();
                    else break;
                }
                tot--;
                if(st.size() < k) st.push(nums[i]);
            }
        }else return "";
        
        while(!st.isEmpty()) {
            ans.append(st.pop());
        }
        return ans.reverse().toString();
    }
	//类似归并排序的过程，合并两个字符串
    String merge(String a,String b){
        StringBuffer ans = new StringBuffer();
        if(a.length()==0) return b;
        if(b.length()==0) return a;
        int aindex = 0;
        int bindex = 0;
        while(aindex < a.length() && bindex < b.length()){
            if(a.charAt(aindex) > b.charAt(bindex)) ans.append(a.charAt(aindex++));  
            else if(a.charAt(aindex) < b.charAt(bindex)) ans.append(b.charAt(bindex++)); 
            //当字符串当前字符相同时候，必须接着比较后序元素，例如a=[604]=[67]
            else if(a.charAt(aindex) == b.charAt(bindex)){
                int astart = aindex+1;
                int bstart = bindex+1;
                boolean flag = false;
                while(astart < a.length() && bstart<b.length()){
                    flag = false;
                    if(a.charAt(astart) == b.charAt(bstart)){
                        astart++;
                        bstart++;
                    }else if(a.charAt(astart) < b.charAt(bstart)){
                        flag = true;
                        ans.append(b.charAt(bindex++));
                        break;
                    }else{
                        ans.append(a.charAt(aindex++));
                        flag = true;
                        break;
                    }
                }
                if(astart==a.length()&&bstart<b.length()) ans.append(b.charAt(bindex++));
                else if(astart<a.length()&&bstart==b.length()) ans.append(a.charAt(aindex++));
                else if(flag == false) ans.append(a.charAt(aindex++));
            }
        }     
        while(aindex<a.length()) ans.append(a.charAt(aindex++));
        while(bindex<b.length()) ans.append(b.charAt(bindex++));
        return ans.toString();
    }
	//对比两个字符串的大小，取大者
    String cmp(String a,String b){
        if(a.length()==0) return b;
        if(b.length()==0) return a;
        for(int i = 0; i < a.length(); i++){
            if(a.charAt(i) < b.charAt(i)) return b;
            else if(a.charAt(i) > b.charAt(i)) return a;
        }
        return a;
    }

    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        String a1 = "";
        String a2 = "";
        String ans = "";
        for(int i = 0; i <= k; i++){
            if(i <= len1 && k-i <= len2){
                a1 = pickMax(nums1,i);
                a2 = pickMax(nums2,k-i);
                //System.out.println("a1:"+a1);
                //System.out.println("a2:"+a2);
                String temp = merge(a1,a2);
                //System.out.println(temp);
                ans = cmp(ans,temp);
                //System.out.println("dd:"+ans);
            }
            
        }
        int p[] = new int[ans.length()];
        for(int i = 0; i < p.length;i++) p[i]=ans.charAt(i)-'0';
        return p;
    }
}

//参考答案2
class Solution {
    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int m = nums1.length;
        int n = nums2.length;
        int[] ans = new int[k];
        int len = Math.min(k, m);
        for (int i=Math.max(0, k-n); i<=len; i++) {
            int[] sub1 = maxKArray(nums1, i);
            int[] sub2 = maxKArray(nums2, k-i);
            int[] array = combineArray(sub1, sub2, k);
            for (int j=0; j<k; j++) {
                if (array[j] == ans[j]) continue;
                if (array[j] > ans[j])  ans = array;
                break;
            }
        }
        return ans;
    }
    
    public int[] maxKArray(int[] nums, int k) {
        if (k == 0) return new int[0];
        
        int[] res = new int[k];
        int cursor = -1;
        for (int i=0; i<nums.length; i++) {
            while (cursor>=0 && nums[i]>res[cursor] && nums.length-i>k-cursor-1) {
                cursor--;
            }
            if (cursor < k-1)
                res[++cursor] = nums[i];
        }
        return res;
    }
    
    public int[] combineArray(int[] nums1, int[] nums2, int k) {
        int[] res = new int[k];
        int i = 0;
        int i1 = 0;
        int i2 = 0;
        while (i1 < nums1.length && i2 < nums2.length)
            res[i++] = deepCompare(nums1, nums2, i1, i2)? nums1[i1++] : nums2[i2++];
        while (i1 < nums1.length)
            res[i++] = nums1[i1++];
        while (i2 < nums2.length)
            res[i++] = nums2[i2++];
        return res;
    }

    public boolean deepCompare(int[] nums1, int[] nums2, int i1, int i2) {
        while (i1 < nums1.length && i2 < nums2.length) {
            if (nums1[i1] == nums2[i2]) {
                i1++;
                i2++;
                continue;
            }
            return nums1[i1] > nums2[i2];
        }
        return i1 < nums1.length;
    }
}



作者：chidehang
链接：https://leetcode-cn.com/problems/create-maximum-number/solution/java-chai-fen-zi-wen-ti-he-bing-qiu-jie-by-chideha/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。