课程主页：http://cs231n.stanford.edu/
loss function:
－Multiclass SVM loss:
表示实际应该属于的类别的score。因此，可以发现，如果实际所属的类别score越小，那么loss function算出来的就会越大，这样才符合常理。
最后取平均：
＊问题：
1⃣️：
因为include j＝y_i其实就是最后加上常数1，对结果没有任何影响。
2⃣️：
因为mean和sum成正比，因此对最后的结果都没影响，所以为了方便计算，无需求mean。
这两种loss function结果会有所区别，但两者都可以。第一种更常见。
min：0（最完美的）
max：正无穷（最不完美的）
和
都很小，所以结果会是number_of_classes - 1.
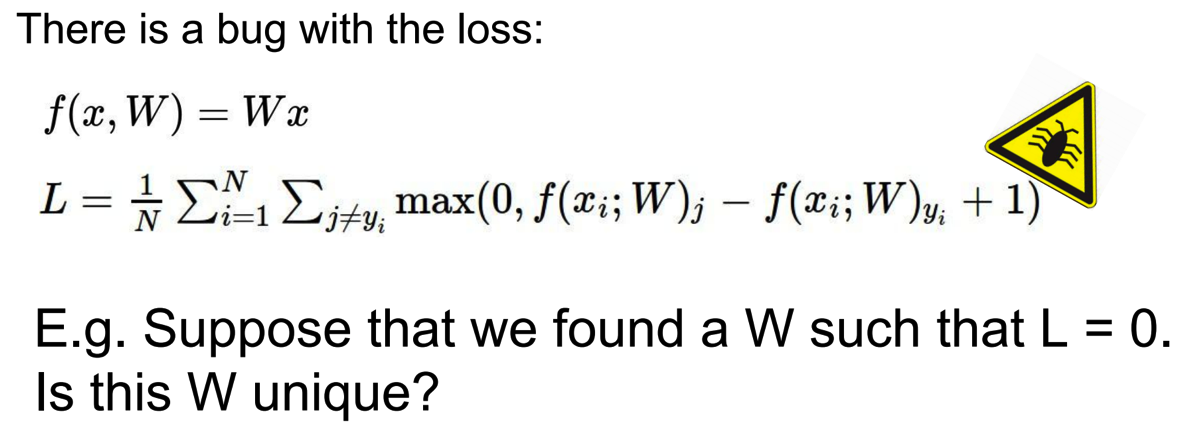
如果每个的都分队的话，w无论乘以多少倍（w不唯一），结果都是一样的。
在w不唯一的情况下，我们如何得到我们最想要的一组w的值呢？因此，我们需要一种方法可以measure niceness of w.
正则化的目的是防止过拟合。
－引出：Weight Regularisation
我们不仅仅想要w能够很好的拟合数据，而且还想得到更好的w。
motivation：
w1只与一个feature有关，忽略了其他的feature。虽然w1和w2的值相同。(详细的介绍参考cs229)
__________________________________________________________________________________________________________
－Softmax function(a different form loss function：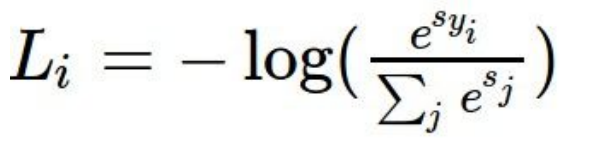
)
（之前用的是svm，即：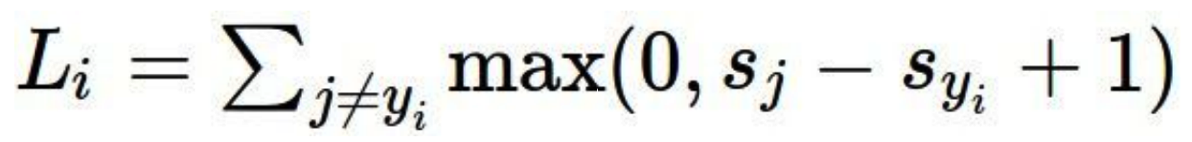
）
计算方法：
＊问题：
min:0 (全部分对)
max:无穷大 （严重分错）
所以，最大值和最小值是一样的，也符合常理。
比较：
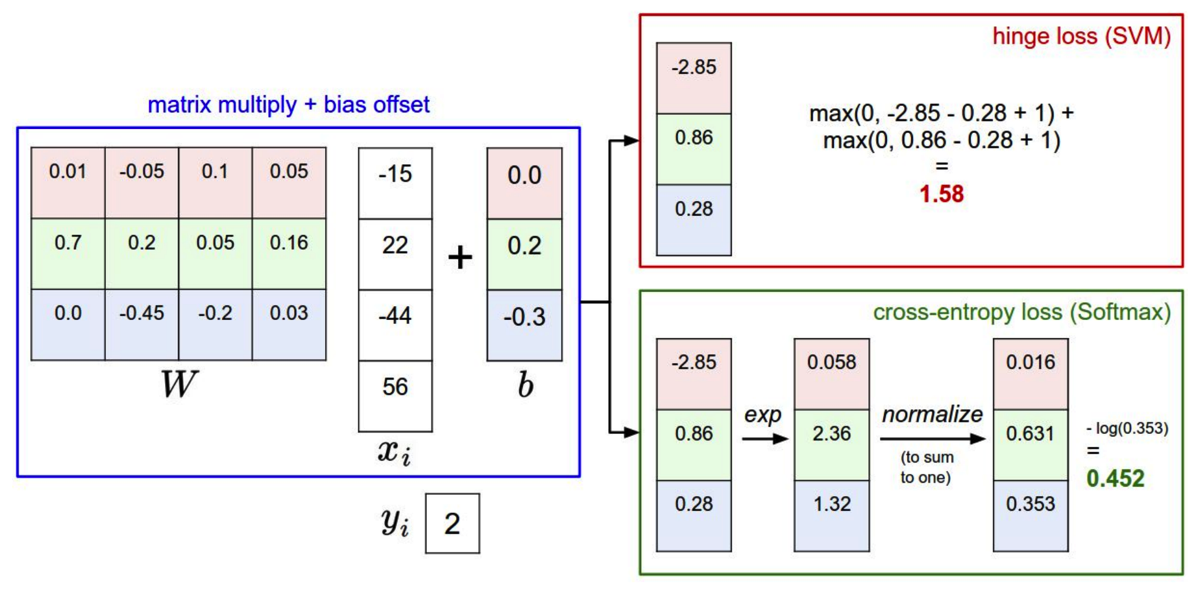
问题：
10是正确的score。
如果把第三个数据[10,-100,100]稍微变一下，两种loss function会有什么样的变化？
svm：会保持不变，因为根据公式里，只要(-x)-(100)+1<0,它都会被认为是0.所以，对结果不会产生任何影响。
softmax：会产生better loss。
有学生提问：为什么是svm中是＋1，可以改为0吗？
回答：必须要一个正数（详细解释请看cs229，margin）
demo : http://vision.stanford.edu/teaching/cs231n/linear-classify-demo/
_________________________________________________________________________________________________________________________________
-Optimization
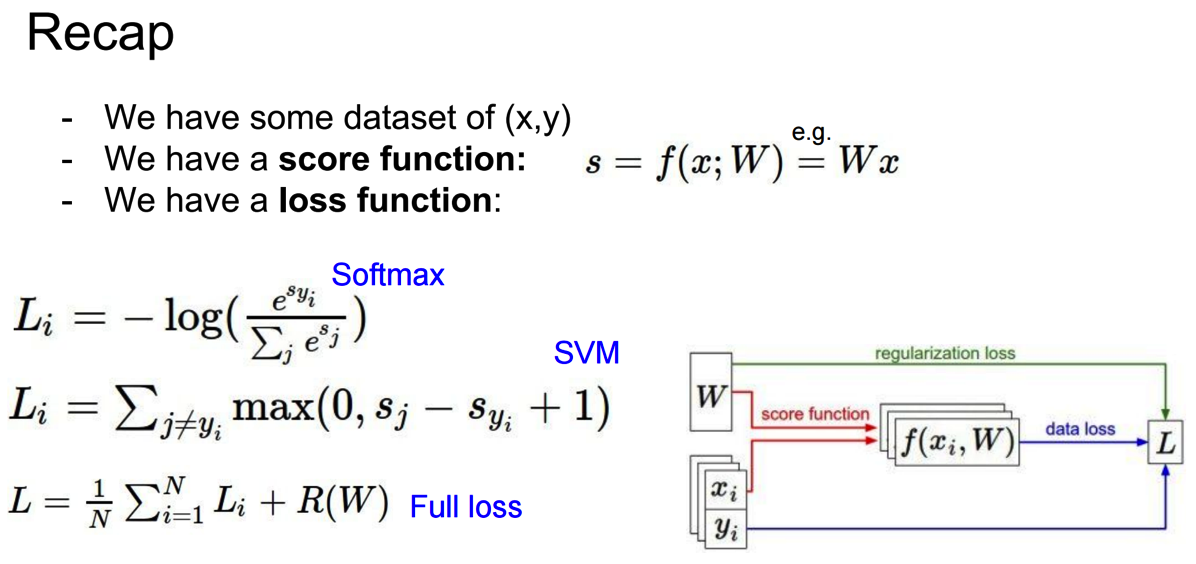
因为参数有成千上万个，如果改变一个参数计算一次loss的话，会非常耗时。
引出微积分（莱布尼茨和牛顿发现的）：
通过直接计算导数就可以了。
总结：
更有效的方法：不把所有的训练数据拿来训练，而是每次随机抽取部分数据拿来训练。虽然每次的结果会有波动，但是总的趋势是下降的。
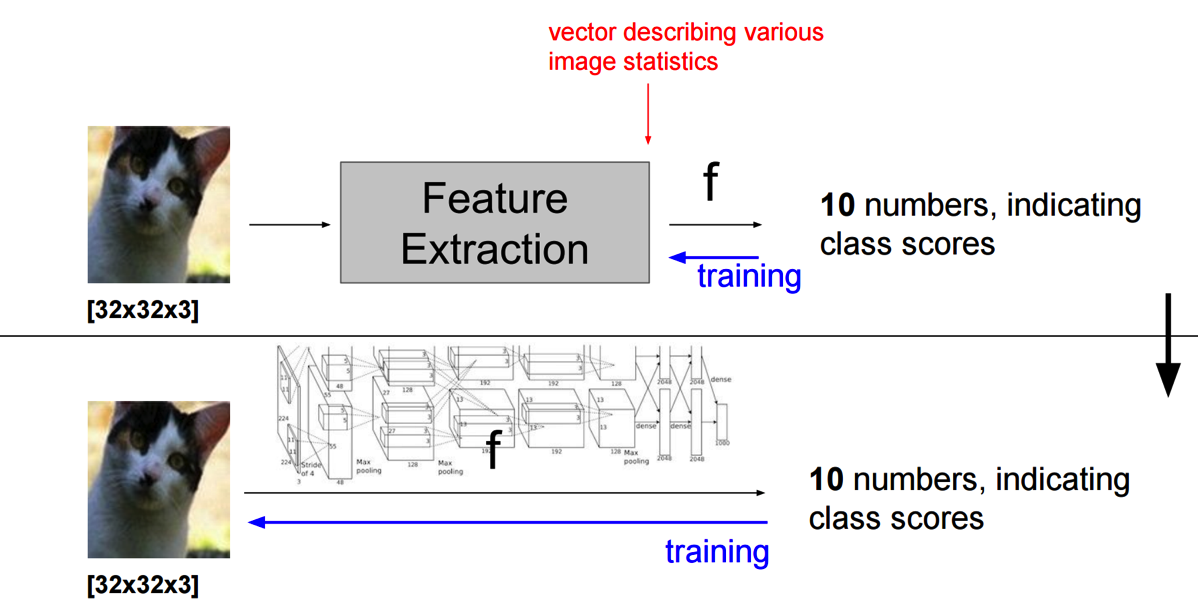
下面的那种不需要feature extraction，直接training出10numbers。
