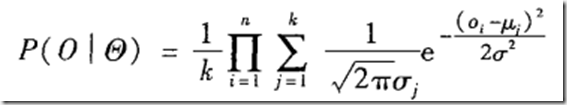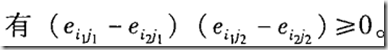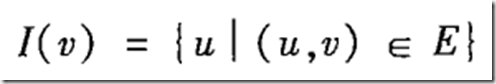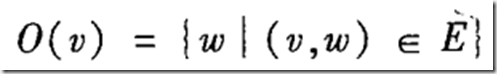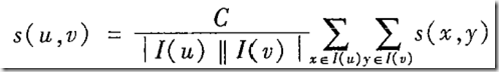1 基于概率模型的聚类
例子：
a.评论产品，一个评论可能设计多种产品，如一个评论谈论摄像机与计算机的兼容性，怎么办？该评论与这两个簇相关，而并不互斥地属于任何一个簇。
b.用户在购买商品时，检索的信息中既订购了一部数据相机，并且同时比较了多种笔记本电脑，怎么办？这种会话应该在某种程度上数据这两个簇。
1.1 模糊簇
这节的例子还不错。
1.2 基于概率模型的聚类
对象以概率的方法参与多个簇。
混合模型假定观测对象集是来自多个概率簇的实例的混合。
以单变量高斯混合模型为例，假定每个簇的概率密度函数都服从一维高斯分布。每个簇都有相同的概率，使用单变量高斯混合模型的基于概率模型的聚类分析任务是推断
，使得下式最大化:
1.3 期望最大化算法——EM算法（结合之前的笔记）
结合之前的K-means方法：
如何把EM算法应用于之前的高斯混合模型呢？
2 聚类高维数据
2.1 聚类高维数据：问题、挑战和主要方法
挑战：
a.数据空间常常太大；
b.不仅需要发现簇，还需要对每个簇找出显露该簇的属性值
2.2 子空间聚类方法
a.子空间搜索方法
b.基于相关性的聚类方法
eg.PCA——主成份分析
c.双聚类方法
2.3 双聚类
1 应用实例
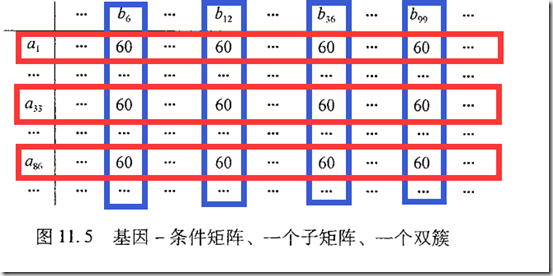
所谓的双聚类就是指对象和属性以对称的方式定义，其中数据分析设计搜索矩阵，寻找作为簇的唯一模式的子矩阵。
推荐系统的例子比较好理解：
2 双簇的类型
双簇：一个子矩阵，其中横纵两维都遵循一致的模式，我们可以基于这种模式定义不同双簇的类型：
a.具有常数值的双簇；
b.行上/列上具有常数值的双簇；
c.具有相干值的双簇；
d.行上/列上相干演变的双簇；
3 双聚类方法
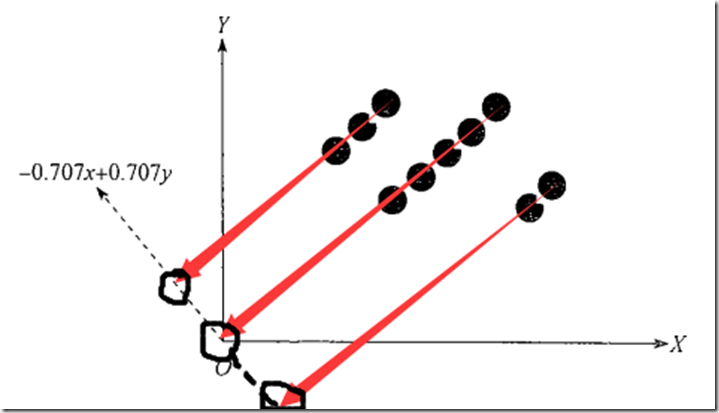
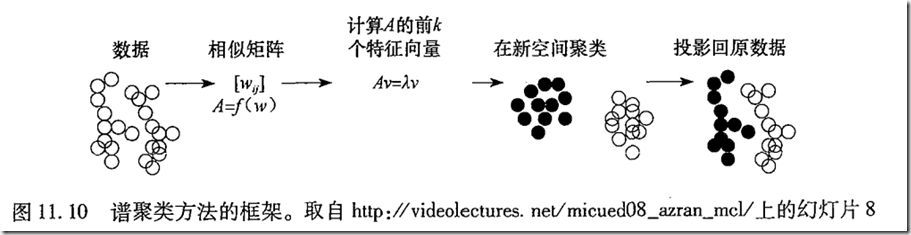
2.4 维规约方法和谱聚类
构造一个新的空间
谱聚类的一般框架：
3 聚类图和网络数据
3.1 应用与挑战
3.2 相似性度量
a.测地距——离心率计算
b.SimRank：基于随机游走和结构情境的相似性
直观意义：图中两个顶点是相似的，如果它们与相似的顶点相链接。为了度量这种相似性，我们需要定义个体的领域的概念，包括入领域和出领域。
入领域：
出领域：
相似度：
simrank：
3.3 图聚类方法
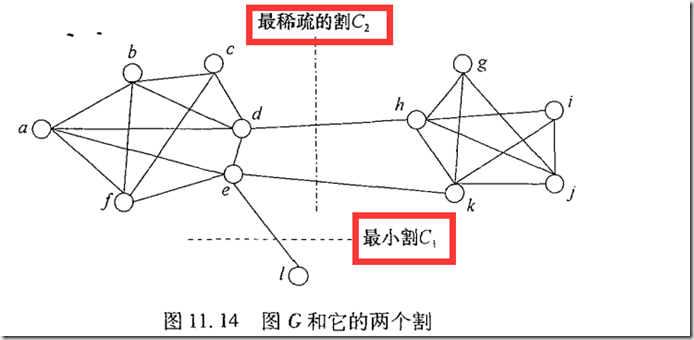
最小割：
最小割未必导致好的聚类。割的稀疏性定义：
聚类的模块性定义——用于评估聚类的质量
图聚类问题都可以看作在图中找最好的割，如最稀疏的割。挑战：
a.高计算开销；
b.复杂的图；
c.高维性；
d.稀疏性；
解决方法：
a.使用聚类高维数据的方法；
使用相似性度量，从图中提取出相似度矩阵，在相似度矩阵上使用一般的聚类方法发现簇。许多情况下，一旦得到相似度矩阵，就可以使用谱聚类方法。谱聚类可以逼近最优图割解。
b.专门为图聚类设计的方法；
搜索图，找出梁联通的成份作为簇。以SCAN(Structrue Clustering Algorithm for Networks , 网络的结构聚类算法)方法为例：
SCAN用规范化的公共领域大小来度量两个顶点u,v之间的相似性：
SCAN算法：
SCAN的一个优点：时间复杂性关于边数是线性的。在大的稀疏图上，边数与顶点数在同一数量级。因此，在大型图上，SCAN可望具有好的可伸缩性。
4 具有约束的聚类
4.1 约束的分类
4.2 具有约束的聚类方法
a.处理硬性约束：
Ⅰ.对必须联系约束产生超实例；
Ⅱ.进行修改后的k-均值聚类，在聚类的过程中，在保证不违反约束的前提下，寻求最优。
b.处理软性约束：（优化问题，总体目标函数是聚类质量得分和罚得分的组合）
Ⅰ.违反必须联系的罚；
Ⅱ.违反不能联系的罚。
c.加快约束聚类的速度
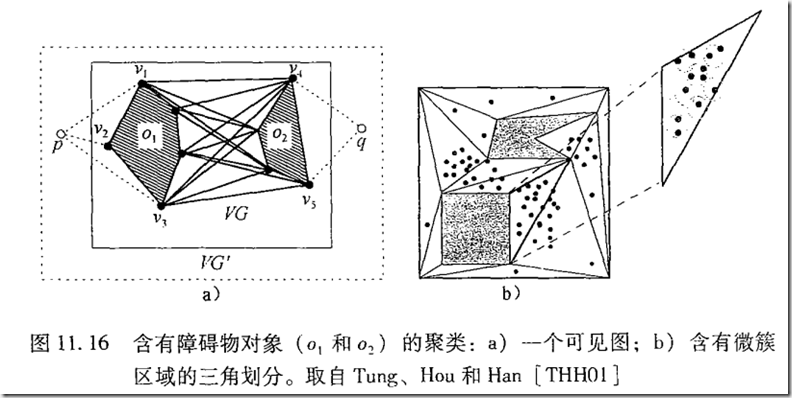
Ⅰ.首先聚集到一些微簇中：划分三角--->把同一个三角形中相似的点聚集到微簇中--->执行预计算来构造两种基于最短路径计算的连接索引
