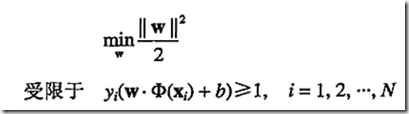ref: blog:http://zhihaozhang.github.io/2014/05/20/svm4/
《数据挖掘导论》
真正的大神是当采用的算法表现出不是非常好的性能的时候,懂得如何去更改算法的人。
本节课的三个内容:
- Kernels:核,用于构建非线性的分类器
- Soft Margin:软间隔,减小噪声对分类的影响
- SMO算法:
1:核
当我们遇到左边的数据,显然,通过一条线是无法讲两种类别分开,那么,为什么利用核技术就可以呢?
a:属性变换
说的通俗一些,就是原来用变量一个变量表示,现在用两个或者多个变量表示,这样做的好处是什么呢?
显然,这样变量的“表现能力”更强大了,而且,不再局限于原始的维数。但是,也会带来一些问题:如更高维时,计算量会增加,维数灾难。
当然,这里还有一个相似度的概念,一个变量表示和多个向量表示,虽然表现能力更强大了,但是,必须要相似,不然就失去了映射的意义。
b:学习非线性SVM模型
问题转化为:
c:核技术
d:Mercer定理
2:软间隔
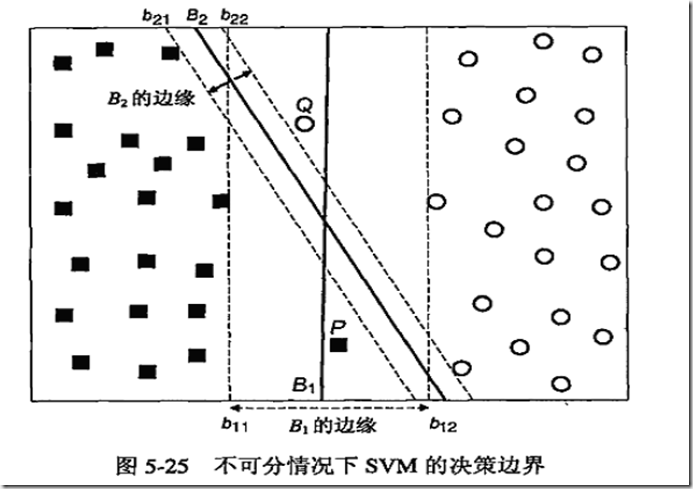
之前的SVM公式只能构造没有错误的决策边界,利用软间隔,我们可以“原谅”一些错误的存在。避免一些噪声的影响,上图中,我们认为B1作为分类超平面比B2更加适合。
a:松弛变量
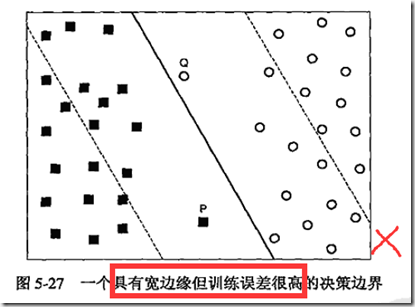
那么,问题来了,我们能够容忍多大的误差呢?这里有个度,如下图:
显然,这种属于不能忍的情况。
b:KKT
3:SMO算法
a:坐标上升算法(coordinate assent algorithm)
由于种种原因,同时优化所有变量不太可能,为了得到全局最优,一次只优化一个变量,而保持其他变量不动的方法。这种方法可行的原因是通常优化一个变量的效率高且算法会比较容易实现。
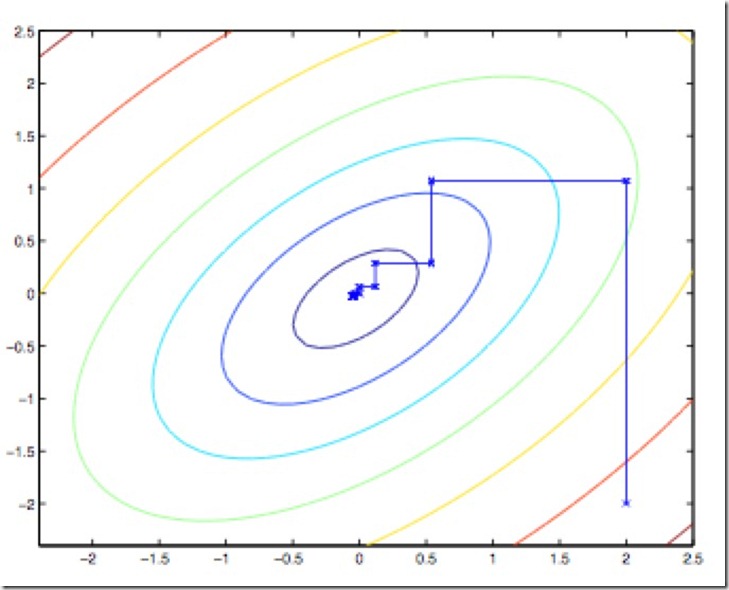
特别地,当只有x,y两个变量的时候,优化的过程如下图:
图中的直线迭代优化的路径,可以看到每一步都会朝着最优解前进一小步,前进的路线是沿着坐标轴方向的,因为每一次都只优化一个变量,而保持另一个变量不变。
b:SMO算法
简化版SMO算法
和坐标上升法的思想类似,SMO算法也想每次只更新一个变量,但是很可惜,
上式限定了,当固定其他所有参数,那么α1上也是个定值,变不了;因此不得不将多增加一个αi,这样α1才能变动,关于αi的选择,有启发式方法,这里先不考虑,介绍一种简单的SMO实现方法。
简化版SMO算法的主要步骤
创建一个alpha向量并将其初始化为0向量 当迭代次数小于最大迭代次数时(外循环) 对数据集中的每个数据向量(内循环): 如果该数据向量可以被优化: 随机选择另一个数据向量 同时优化这两个向量
如果两个向量都不能被优化,退出内循环
如果所有向量都没有被优化,增加迭代数目,继续下一次循环
如何更新α
SMO之所以高效是因为,当固定了其他参数后,对一个参数的优化过程很高效,现在我们就来看看到底怎么优化这一个参数。
假设我们选取了初始值{α1,α2,…,αn}并且满足KKT条件,下面固定{α3,…,αn},这样W就是α1,α2的函数,而α1,α2满足条件:
为了方便,我们将等式右边的常数值表示为k。
根据y1、y2符号是否相同,可以分为以下两种情况:
接下来以左边的图为例,来说明以下α的选取范围。
当y1、y2异号时,直线的斜率是1,由于KKT条件限定了α1、α2的范围必须在边长为c的正方形内,因此直线有下面两种可能性,
从图中不难总结出取值的上限H和下限L:
L=max(0,α2-α1),H=min(C,C+α2-α1)
同理,y1、y2同号时,
L=max(0,α2+α1-c),H=min(C,α2+α1)
将α1用α2来表示,带回W中,W会被表示成一个二次函数,a(α2)^2+bα2+c,二次函数求最值问题是高中最常做的一个问题了,基本思想是数形结合,找对称轴,然后看变量的取值范围里是否包含了对称轴,如下图:
根据能否取得对称轴,我们可以得到以下更新α2的原则:
有了α2,求解新的α1就不是难事了。