Rancher's Gift
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 26 Accepted Submission(s): 21
Problem Description
Rancher Joel has a tract of land in the shape of a convex quadrilateral that the wants to divide among his sons Al, Bob, Chas and Dave, who wish to continue ranching on their portions, and his daughter Emily, who wishes to grow vegetables on her portion.
The center of the tract is most suitable for vegetable farming so Joel decides to divide the land by drawing lines from each corner (A, B, C, D in counter clockwise order) to the center of an opposing side (respectively A', B', C' and D') Each son would receive one of the triangular sections and Emily would receive the central quadrilateral section. As shown in the figure, Al's tract is to be bounded by the line from A to B, the line from A to the midpoint of BC and the line from B to the midpoint of CD' Bob&s ract is to be bounded by the line from B to C, the line from B to the midpoint of CD and the line from C to the midpoint of DA, and so on.
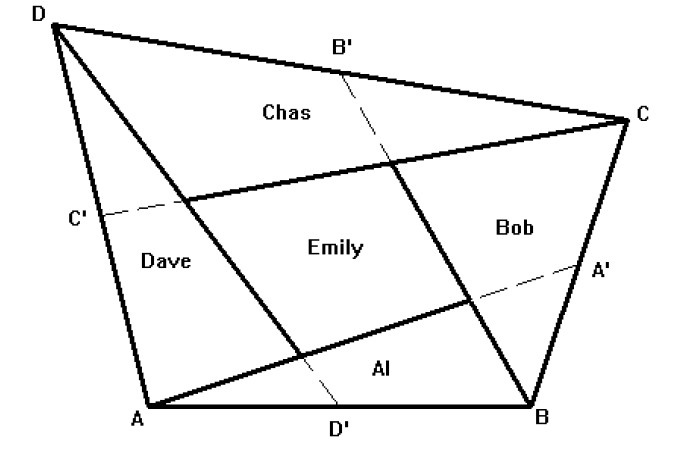
Your job is to write a program that will help Rancher Joel determine the area of each child's tract and the length of the fence he will have to put around Emily's parcel to keep her brothers' cows out of her crops.
For his problem, A will always be at (0, 0) and B will always be at (x, 0). Coordinates will be in rods (a rod is 16.5 feet).The returned areas should be in acres to 3 decimal places (an acre is 160 square rods) and the length of the fence should be in feet, rounded up to the next foot.
The center of the tract is most suitable for vegetable farming so Joel decides to divide the land by drawing lines from each corner (A, B, C, D in counter clockwise order) to the center of an opposing side (respectively A', B', C' and D') Each son would receive one of the triangular sections and Emily would receive the central quadrilateral section. As shown in the figure, Al's tract is to be bounded by the line from A to B, the line from A to the midpoint of BC and the line from B to the midpoint of CD' Bob&s ract is to be bounded by the line from B to C, the line from B to the midpoint of CD and the line from C to the midpoint of DA, and so on.

Your job is to write a program that will help Rancher Joel determine the area of each child's tract and the length of the fence he will have to put around Emily's parcel to keep her brothers' cows out of her crops.
For his problem, A will always be at (0, 0) and B will always be at (x, 0). Coordinates will be in rods (a rod is 16.5 feet).The returned areas should be in acres to 3 decimal places (an acre is 160 square rods) and the length of the fence should be in feet, rounded up to the next foot.
Input
The first line of input contains a single integer P( 1 <= P <= 1000),which is the number of data sets that follow. Each data set is a single line that contains of a decimal integer followed by five (5) space separated floating-point values. The first (integer) value is the data set number, N. The floating-point values are B.x, C.x, C.y, D.x and D.y in that order (where V.x indicates the x coordinate of V and V.y indicates the y coordinate of V). Recall that the y coordinate of B is always zero (0). The supplied coordinates will always specify a valid convex quadrilateral.
Output
For each data set there is a single line of output. It contains the data set number, N , followed by a single space followed by five(5) space separated floating-point values to three(3) decimal place accuracy, followed by a single space and a decimal integer! The floating-point values are the areas in acres of the properties of Al, Bob, Chas, Dave, and Emily respectively. The final integer is the length of fence in feet required to fence in Emily's property (rounded up to the next foot).
Sample Input
3 1 200 250 150 -50 200 2 200 200 100 0 100 3 201.5 157.3 115.71 -44.2 115.71
Sample Output
1 35.000 54.136 75.469 54.167 54.666 6382 2 25.000 25.000 25.000 25.000 25.000 4589 3 29.144 29.144 29.144 29.144 29.144 4937
Source
求四边形分割成五块区域的面积以及求中间区域的周长
哈哈,神奇的A了!
code:
1 #include<iostream> 2 #include<cmath> 3 using namespace std; 4 5 struct node 6 { 7 double x,y; 8 }node[100]; 9 10 double area[5]; 11 double t1,t2,t3,t4,t5; 12 double areasum; 13 double lensum; 14 double fun4(int cur1,int cur2); 15 void fun(int cur,double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) 16 { 17 node[cur].x=((x1-x2)*x4*(y3-y4)-x2*(x3-x4)*(y1-y2)+(y2-y4)*(x1-x2)*(x3-x4))/((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4)); 18 node[cur].y=(((x4-x2)*(y1-y2)+(y2-y4)*(x1-x2))*(y3-y4)+y4*(((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4))))/((x1-x2)*(y3-y4)-(y1-y2)*(x3-x4)); 19 } 20 21 double ab_s(double a) 22 { 23 if(a<0) 24 { 25 return -a; 26 } 27 return a; 28 } 29 30 double funt(double x1,double y1,double x2,double y2) 31 { 32 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 33 } 34 35 void fun1(int cur,double x1,double y1,double x2,double y2,double x,double y) 36 { 37 double d; 38 double len1,len2,len3,p; 39 len1=funt(x1,y1,x2,y2); 40 len2=funt(x1,y1,x,y); 41 len3=funt(x2,y2,x,y); 42 p=(len1+len2+len3)/2.0; 43 area[cur]=sqrt(p*(p-len1)*(p-len2)*(p-len3)); 44 } 45 46 double funw(double x1,double y1,double x2,double y2,double x,double y) 47 { 48 double d; 49 double len1,len2,len3,p; 50 len1=funt(x1,y1,x2,y2); 51 len2=funt(x1,y1,x,y); 52 len3=funt(x2,y2,x,y); 53 p=(len1+len2+len3)/2.0; 54 return sqrt(p*(p-len1)*(p-len2)*(p-len3)); 55 } 56 57 void fun2() 58 { 59 double t1,t2; 60 t1=funw(node[0].x,node[0].y,node[1].x,node[1].y,node[3].x,node[3].y); 61 t2=funw(node[1].x,node[1].y,node[2].x,node[2].y,node[3].x,node[3].y); 62 areasum=t1+t2; 63 areasum-=(area[0]+area[1]+area[2]+area[3]); 64 } 65 66 void fun3() 67 { 68 lensum=(fun4(8,9)+fun4(9,10)+fun4(10,11)+fun4(11,8)); 69 } 70 71 double fun4(int cur1,int cur2) 72 { 73 return sqrt((node[cur1].x-node[cur2].x)*(node[cur1].x-node[cur2].x)+(node[cur1].y-node[cur2].y)*(node[cur1].y-node[cur2].y)); 74 } 75 76 int main() 77 { 78 int t; 79 int cases; 80 scanf("%d",&t); 81 while(t--) 82 { 83 memset(node,0,sizeof(node)); 84 scanf("%d%lf%lf%lf%lf%lf",&cases,&t1,&t2,&t3,&t4,&t5); 85 node[0].x=0; 86 node[0].y=0; 87 node[1].x=t1; 88 node[1].y=0; 89 node[2].x=t2; 90 node[2].y=t3; 91 node[3].x=t4; 92 node[3].y=t5; 93 94 95 node[4].x=(t1)/2.0; 96 node[4].y=0;; 97 node[5].x=(t1+t2)/2.0;; 98 node[5].y=t3/2.0; 99 node[6].x=(t2+t4)/2.0; 100 node[6].y=(t3+t5)/2.0; 101 node[7].x=t4/2.0; 102 node[7].y=t5/2.0; 103 104 105 fun(8,node[0].x,node[0].y,node[5].x,node[5].y,node[3].x,node[3].y,node[4].x,node[4].y); 106 fun(9,node[0].x,node[0].y,node[5].x,node[5].y,node[1].x,node[1].y,node[6].x,node[6].y); 107 fun(10,node[7].x,node[7].y,node[2].x,node[2].y,node[1].x,node[1].y,node[6].x,node[6].y);; 108 fun(11,node[7].x,node[7].y,node[2].x,node[2].y,node[3].x,node[3].y,node[4].x,node[4].y); 109 110 fun1(0,node[0].x,node[0].y,node[1].x,node[1].y,node[9].x,node[9].y); 111 fun1(1,node[1].x,node[1].y,node[2].x,node[2].y,node[10].x,node[10].y); 112 fun1(2,node[2].x,node[2].y,node[3].x,node[3].y,node[11].x,node[11].y); 113 fun1(3,node[3].x,node[3].y,node[0].x,node[0].y,node[8].x,node[8].y); 114 115 fun2(); 116 fun3(); 117 lensum=lensum*16.5; 118 if(lensum!=int(lensum)) 119 lensum=int(lensum)+1; 120 printf("%d %.3f %.3f %.3f %.3f %.3f %.0f\n",cases,area[0]/160,area[1]/160,area[2]/160,area[3]/160,areasum/160,lensum); 121 } 122 return 0; 123 } 124 /* 125 3 126 1 200 250 150 -50 200 127 2 200 200 100 0 100 128 3 201.5 157.3 115.71 -44.2 115.71 129 */