树的相关术语
结点:有一个数据元素及若干指向其他结点的分支所组成
度:结点的度:该结点的子树树(即分支树)
树的度:书中结点的度最大值
叶子(终端结点):度为零的结点
非终端结点:度不为零的结点
孩子(子节点):结点的字数根称为该结点的孩子
双亲(父节点):一个结点称为该节点所有子树根的双亲
祖先:结点祖先指根道此结点的一条路径上的所有结点
子孙:某结点到叶结点的分支上的所有结点称为该节点的子孙
兄弟:同一双亲的孩子之间互称兄弟
结点层次:从根算起,根为第一层,其孩子在第二层....,L层上任何结点的孩子都在L+1层上。
堂兄弟:其双亲在同一层的结点
树的深度:树中结点的最大层次
有序树:若树中各结点的子树从左到右是有次序的,不能互换,称为有序树
无序树:若树种结点的子树是无次序的,可以互换,则成为无序树
森林:是M>=0棵树的集合
二叉树
定义:
二叉树是n(n>=0)个结点的有限集合,它或为空(n=0),
或是由一个根及两棵互不相交的左子树和右子树组成,且
中左子树和右子树也均为二叉树
特点:
①二叉树可以是空的,称空二叉树;
②每个结点最多只能有两个孩子;
③子树有左、右之分且次序不能颠倒。

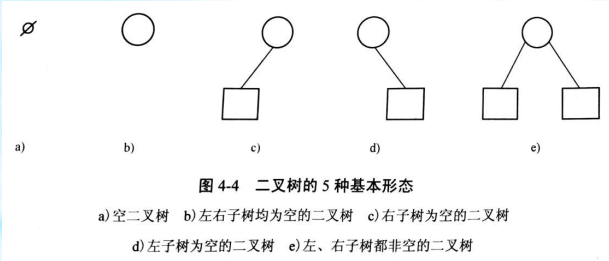
二叉树结点的子树要区分左子树和右子树,即使只有一棵子树也
要进行区分,说明它是左子树,还是右子树。这是二叉树与树的最
主要的差别。下图列出二叉树的5种基本形态,图(C) 和(d)是不
同的两棵二叉树。
二叉树的性质:
1、在二叉树的第I(i>=1)层上之多有2i-1个结点
2、深度为k(k>=1)的二叉树至多有2k-1个结点
3、对任何一颗二叉树,如果其终端结点数为n0,度为2的结点数位n2,则n0=n2+1
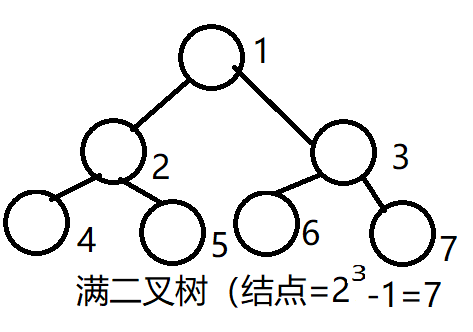
满二叉树——深度为k(k>=1)且有2k-1个结点的二叉树
满二叉树中结点顺序编号:即从第一层结点开始自上而下,从左到右进行连续编号
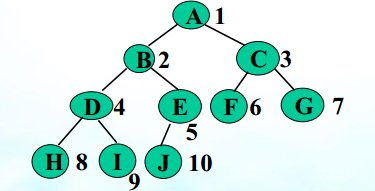
完全二叉树:深度位K的二叉树中,K-1层结点数是满的(2k-2),K层结点是左连续的(即结点编号是连续的)
满二叉树是完全二叉树的特例
4.具有n个结点的完全二叉树的深度为[log2n]+1
5. 对有n个结点的完全二叉树的结点按层编号
(从第1层到第[log2n]+1层,每层从左到右),
则对任一结点i(1≤i≤n),有:
(1) 如果i=1,则结点i无双亲,是二叉树的根;
如果i>1,则i的双亲Parent(A)是结点⌊i/2⌋;
(2) 如果2*i≤n,则其左孩子是结点2*i,
否则,结点i无左孩子且为叶子结点;
(3) 如果2*i+1≤n,则其右孩子是结点2*i+1,
否则,结点i无右孩子
二叉树的顺序存储结构
它是用一组连续的存储单元存储二叉树的数据元素。因此,必须把二叉树的所有结点安排成为一个恰当的序列,结点在这个序列中的相互位置能反映出结点之间的逻辑关系,可用编号的方法。
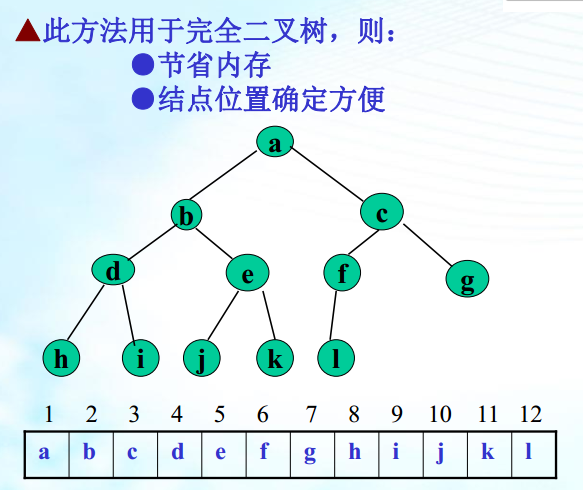
二叉树的顺序存储结构——即对二叉树按完全二叉树进行编号,然后用一维数组存储,其中编号为i的结点存储在数组中下标为i的分量中。
——该方法称为“以编号为地址” 策略

二叉树的链式存储结构
二叉链表示法 :左边指针是左孩子 ,右边指针是右孩子
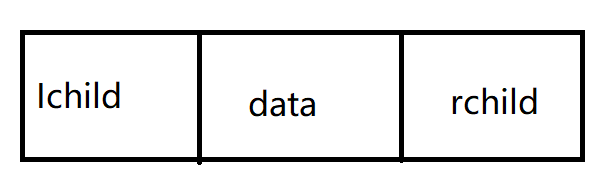
1 二叉链表类型定义 2 typedef struct btnode { 3 DataType data; 4 struct btnode *lchild,*rchild; 5 }*BinTree;;

在含n个结点的二叉链表中有2n个指针域,其中n-1个用来指向结点的左右孩子,其余n+1个空链域