Description
In the year 2051, several Mars expeditions have explored different areas of the red planet and produced maps of these areas. Now, the BaSA (Baltic Space Agency) has an ambitious plan: they would like to produce a map of the whole planet. In order to calculate the necessary effort, they need to know the total size of the area for which maps already exist. It is your task to write a program that calculates this area.
Task Write a program that:
- reads the description of map shapes from the input file mar.in,
- computes the total area covered by the maps,
- writes the result to the output file mar.out.
题目大意:给你N个矩形,给出矩形对角坐标,要你求出这些矩形所覆盖的面积
Input
The input file mar.in starts with a line containing a single integer N (1<=N<=10 000) the number of available maps. Each of the following N lines describes a map. Each of these lines contains four integers x1, y1, x2 and y2 (0<=x1the coordinates of, respectively, the bottom-left and the top-right corner of the mapped area. Each map has rectangular shape, and its sides are parallel to the x- and y-axis of the coordinate system.
Output
The output should contain one integer A, the total explored area
(i.e. the area of the union of all rectangles).
Sample Input
2
10 10 20 20
15 15 25 30
Sample Output
225
这道题目是一个比较经典的题目,它用到了线段树扫描线这个方法。
扫描线是什么东西?
首先我们给出一张图,图中共有3个矩形,覆盖的总面积为24。
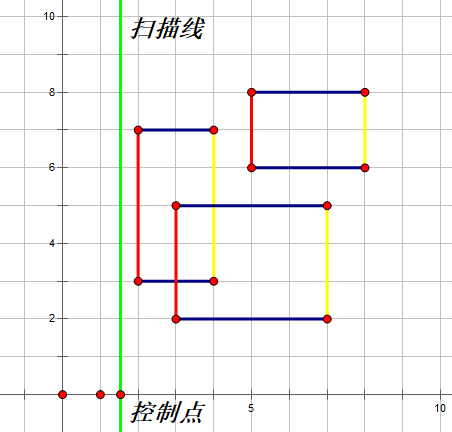
图中绿色的线即为扫描线。线段树上维护的信息为扫描线上的区间是否被覆盖。
扫描线从左方向右方移动,图中红色的边叫做起始边,黄色的边叫做终止边。在扫描线不断扫描的过程中,碰到起始边,我们就将起始边覆盖上去;碰到终止边时,就从扫描线上将其抹去。
这样做有什么用?
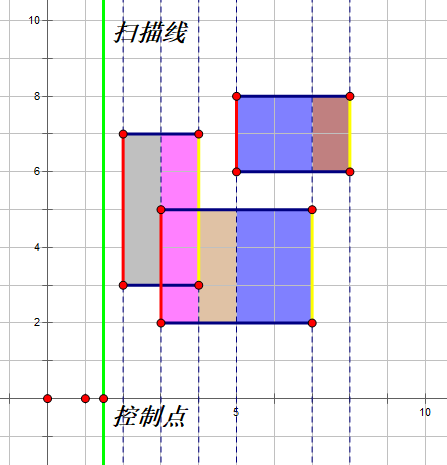
我们把关建边(起始边和终止边的统称)所在的位置标明出来。每两个关建边之间都有一段面积(图中相同颜色的为同一段),这些面积之和即为总覆盖面积。这些面积怎么算?
其实相信大家心中已经有了答案。
每一小段的面积,就是上一个关建边操作完之后,线段树上覆盖区间大小乘上两个关建边之间的距离。
所以接下来就是傻逼的处理和线段树的维护了。
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x>=10) print(x/10);
putchar(x%10+'0');
}
const int N=5e4;
struct AC{
int l,r,val,ID;
bool operator <(const AC &x)const{return val!=x.val?val<x.val:ID>x.ID;}//按横坐标排序,起始边要摆在终止边之前。至于为什么,见文章底
}A[N];
struct Segment{
#define ls (p<<1)
#define rs (p<<1|1)
int tree[N*16+10],Lazy[N*16+10];//线段树记录的就是一个个区间,而不是一个个坐标,因此主程序中使用r-1
void updata(int p,int l,int r){//区间覆盖大小的维护
if (Lazy[p]) tree[p]=r-l+1;
else tree[p]=(l==r)?0:(tree[ls]+tree[rs]);
}
void change(int p,int l,int r,int x,int y,int t){//简单打标记
if (x<=l&&r<=y){
Lazy[p]+=t;
updata(p,l,r);
return;
}
int mid=(l+r)>>1;
if (x<=mid) change(ls,l,mid,x,y,t);
if (y>mid) change(rs,mid+1,r,x,y,t);
updata(p,l,r);
}
}T;
int main(){
int n=read(),ans=0;
for (int i=1;i<=n;i++){
int a=read(),b=read(),c=read(),d=read();
A[i].ID=1,A[i+n].ID=-1;//ID记录是起始边还是结束边
A[i].val=a, A[i].l=b, A[i].r=d-1;//按关建边的x坐标排序,因此要记录,l,r即为区间左右边界
A[i+n].val=c,A[i+n].l=b,A[i+n].r=d-1;
}
sort(A+1,A+1+2*n);
for (int i=1;i<=2*n;i++){
if (i!=1) ans+=(A[i].val-A[i-1].val)*T.tree[1];//i=1的时候没有什么东西可以加
T.change(1,-N,N,A[i].l,A[i].r,A[i].ID);
}
printf("%d
",ans);
return 0;
}
为什么在排序的时候,起始边要在终止边前面呢?
其实对于本题而言,并没有什么影响。
不过起始边和终止边的摆放位置对下一题有影响。
请参考[IOI1998]Picture