Description
Find the biggest integer (n (1leqslant nleqslant N)) and an integer (x) to make them satisfy
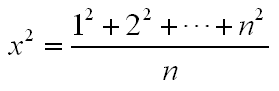
Input
The input consists of several test cases. Each test case contains a integer (N, 1leqslant Nleqslant 10^{18}).The input ends with (N = 0).
Output
In one line for each case, output two integers (n) and (x) you have found.
Sample Input
1
2
0
Sample Output
1 1
1 1
根据自然数幂和可得 (sumlimits_{i=1}^ni^2=frac{n(n+1)(2n+1)}{6}),将其代入原式可得 (x^2=frac{(n+1)(2n+1)}{6})
移项配方可得((4n+3)^2-48x^2=1),满足Pell方程的形式,故可直接套用
关于Pell方程的详细推导及证明,由于本人未能看懂,故不在此赘述,兴趣可以参考以下几个链接
https://blog.csdn.net/u011815404/article/details/88717125
https://blog.csdn.net/ddaarsel63181/article/details/102408570
https://baike.baidu.com/item/佩尔方程/11029962?fr=aladdin#2_3
/*program from Wolfycz*/
#include<map>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define ll_inf 1e18
#define MK make_pair
#define pll pair<ll,ll>
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define int_inf 0x7f7f7f7f
#define pdd pair<double,double>
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
static char buf[1000000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
int f=1; char ch=gc();
for (;ch<'0'||ch>'9';ch=gc()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
template<typename T>inline T read(T x){
int f=1; char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+'0');
}
const int D=48;
vector<pll>vec,Ans;
void prepare(){
vec.push_back(MK(7ll,1ll));
Ans.push_back(MK(1ll,1ll));
while (true){
ll x=vec.back().Fi,y=vec.back().Se;
ll _x=7*x+D*y,_y=x+7*y;
if (_x<0) break;
vec.push_back(MK(_x,_y));
if ((_x-3)%4) continue;
Ans.push_back(MK((_x-3)/4,_y));
}
Ans.push_back(MK((ll)1e18+5,0));
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
prepare(); ll n;
while (scanf("%lld",&n)!=EOF&&n){
for (int i=0;i<(int)Ans.size();i++){
if (Ans[i].Fi>n){
printf("%lld %lld
",Ans[i-1].Fi,Ans[i-1].Se);
break;
}
}
}
return 0;
}