题目传送门:https://agc017.contest.atcoder.jp/tasks/agc017_f
题目大意:
找出(m)个长度为(n)的二进制数,定义两个二进制数的大小关系如下:若(a<b),则设(a_i)表示(a)的二进制下第(i)位(从左往右)的数,有(a_ileqslant b_i,iin[1,n])
现需要满足每个二进制数需要小于其之后的二进制数,并且给出一些性质,满足第(A_j)个二进制数的第(B_j)位(从左往右)必须要为(C_i),求方案数
显然是个DP题,考虑如何DP,我们首先可以想到状压每条路径,设(f_{i,j})表示当前走完第(i)条路径,第(i)条路径的表示为(j),转移时直接枚举下一条路径,时间复杂度(O(2^{2·N}·M)),枚举子集优化可以为(O(3^N·M)),但无论如何都过不了
考虑优化,上一个DP做法的瓶颈在于需要枚举下一条路径的状态,我们考虑不枚举,直接从当前状态下手。设(f_{i,j,k})表示当前正在走第(i)条路径,已经走了(j)步,目前能走的最靠左的路径状态为(k)
我们枚举第(j+1)步向哪边移动,如果要向左走,当前位置状态必须为(0);如果向右走,当前位置状态为(1)时直接走,如果当前位置状态不为零,就把后面位置的一个(1)挪到这里,用位运算可以做到(O(1))转移,复杂度(O(2^N·N·M))
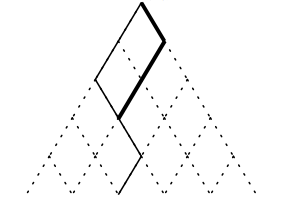
(细线为原本路径,粗线为新路径,相当于将后面的一个(1)提前了)
/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
#define lowbit(x) ((x)&-(x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
static char buf[1000000],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
inline int frd(){
int x=0,f=1; char ch=gc();
for (;ch<'0'||ch>'9';ch=gc()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=gc()) x=(x<<3)+(x<<1)+ch-'0';
return x*f;
}
inline int read(){
int x=0,f=1; char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+ch-'0';
return x*f;
}
inline void print(int x){
if (x<0) putchar('-'),x=-x;
if (x>9) print(x/10);
putchar(x%10+'0');
}
const int p=1e9+7;
int f[2][(1<<20)+10],C[30][30];
int main(){
int n=read()-1,m=read(),k=read();
for (int i=1;i<=k;i++){
int x=read(),y=read(),z=read();
C[x][y-1]=z+1;
}
f[0][0]=1; int now=0;
for (int i=1;i<=m;i++){
for (int j=0;j<n;j++){
now^=1;
memset(f[now],0,sizeof(f[now]));
for (int s=0;s<1<<n;s++){
if (f[now^1][s]){
if (C[i][j]!=2&&((s>>j)&1)==0) f[now][s]=(f[now][s]+f[now^1][s])%p;
if (C[i][j]!=1){
int Ns=0;
if ((s>>j)&1) Ns=s;
else{
int tmp=((-1)^((1<<(j+1))-1))&s,Ds=!tmp?0:lowbit(tmp);
Ns=s^(1<<j)^Ds;
}
f[now][Ns]=(f[now][Ns]+f[now^1][s])%p;
}
}
}
}
}
int Ans=0;
for (int s=0;s<1<<n;s++) Ans=(Ans+f[now][s])%p;
printf("%d
",Ans);
return 0;
}