【原文: https://www.cnblogs.com/fortunely/p/10254161.html】
1.基本概念
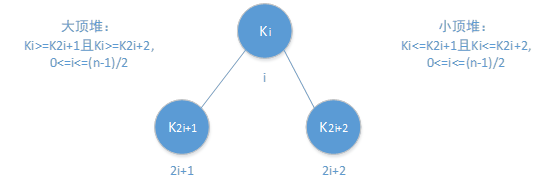
堆,分为大顶堆(大堆)和小顶堆(小堆),是顺序存储的完全二叉树,并且满足以下特性之一:
(1) 任意非终端结点关键字不小于左右子结点(大堆)
ki >= k2i+1并且ki>=k2i+2 其中,0 <= i <= (n-1)/2,n是数组元素个数
(2) 任意非终端结点关键字不大于左右子结点(小堆)
ki <= k2i+1并且ki<=k2i+2 其中,0 <= i <= (n-1)/2,n是数组元素个数
调整(也有叫筛选):
从当前结点(要求是非终端结点)开始,
对于大堆,要求当前结点关键字不小于子结点,如不符合,则将最大的子结点与当前结点交换。循环迭代交换后的子树,确保所有子树都符合大堆特性。

小堆调整过程类似。
2.基本思想
堆排序就是利用构建堆和输出堆顶元素的过程,不断对堆进行调整以保证当前结点及其孩子结点满足堆特性,从而达到对初始数组元素进行排序的目的。
大堆通常对应升序序列,小堆通常对应降序排列。
核心步骤:
1)构建堆(大堆/小堆)
从最后一个非终端结点开始,向前进行调整,保证当前结点及其子树符合堆特性;
2) 输出有序序列
交换堆顶与末尾叶子结点,堆顶输出到数组的有序序列末尾,而不参与堆的调整。从交换后的堆顶开始调整,以确保当前结点及其子树符合堆特性。
3.实例
下面举个例子,利用小堆进行降序排列。
|
初始序列 |
49 |
38 |
65 |
97 |
76 |
13 |
27 |
49‘ |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
3.1.构建堆
1) 初始序列对应初始堆
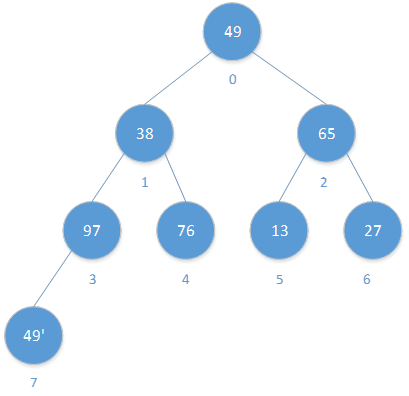
从最后一个非叶子结点开始,向前进行调整,确保符合特性
最后一个非叶子结点位置:(n-1) / 2 = 3, n=8
总共调整次数:(n-1)/2 +1 = 4
第1次调整:选择最后一个非叶子结点元素为97(位置3)为当前父结点,与其子结点进行比较,选择最小的结点作为当前父结点。
|
第1次调整后序列 |
49 |
38 |
65 |
49’ |
76 |
13 |
27 |
97 |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |

第2次调整:选择上一次结点的前一个结点65(位置2)为当前结点进行调整。
|
第2次调整后序列 |
49 |
38 |
13 |
49’ |
76 |
65 |
27 |
97 |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
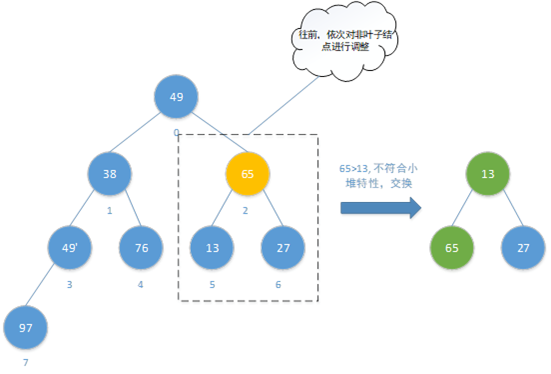
第3次调整:选择上一次结点的前一个结点38(位置1)为当前结点进行调整。
|
第3次调整后序列 |
49 |
38 |
13 |
49’ |
76 |
65 |
27 |
97 |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |

第4次调整:选择上一次结点的前一个结点49(位置0)为当前结点进行调整。
|
第4次调整后序列 |
13 |
38 |
27 |
49’ |
76 |
65 |
49 |
97 |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |

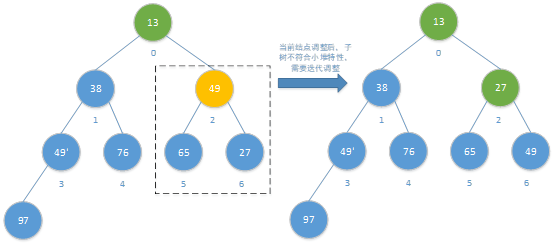
3.2.输出堆顶元素
将已经构建好的小堆,输出堆顶元素,和末尾元素交换,相当于堆顶移动到数组末尾形成有序序列,未排序元素移动到堆顶。从新的堆顶开始进行调整,直到堆重新符合小堆特性。
交换堆顶和末尾(堆的末尾,不包括已经排好序的部分),并将交换后的堆末尾作为有序序列的一部分,而不再属于堆。
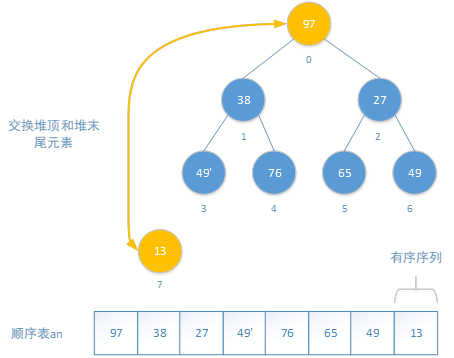
一次交换后,发现97新的位置比子结点大,需要继续调整。
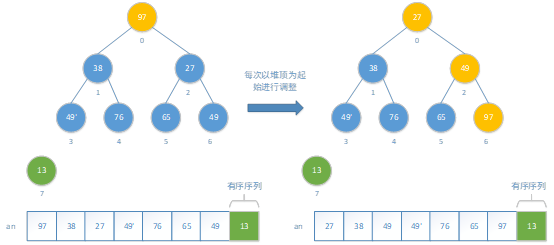
这样,不断输出所有堆顶到数组末尾,最终可以得到
|
有序序列 |
97 |
76 |
65 |
49 |
49’ |
38 |
27 |
13 |
|
位置 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4.实现代码
1 //堆排序(小根堆) 2 3 //i为调整的位置 4 void HeapAdjust(int a[], int i, int len) 5 { 6 if (i > len / 2 - 1) //叶子结点, 无子树 7 { 8 return; 9 } 10 11 // 检查结点i是否符合最大堆特性, 如果不符合, 需要与最大子结点交换 12 for (int k = 2 * i + 1; k < len; k = 2 * k + 1) 13 { 14 // 判断右子树是否比左子树更大 15 if (k + 1 < len && a[k + 1] > a[k]) 16 { 17 k++; // 更新最大子结点 18 } 19 20 if (a[i] < a[k]) 21 { 22 int temp = a[i]; 23 a[i] = a[k]; 24 a[k] = temp; 25 i = k; // 将最大子结点位置设为当前结点 26 } 27 else // 符合大堆特性 28 { 29 break; 30 } 31 } 32 } 33 34 void HeapSort(int arr[], int len) 35 { 36 // 先建堆 37 // 从最后一个非叶子结点开始, 向前进行调整 38 for (int i = (len - 1) / 2; i >= 0; i--) 39 { 40 HeapAdjust(arr, i, len); 41 } 42 43 // 再输出并调整 44 for (int j = len - 1; j > 0; j--) // 判断条件不用加"=", 因为j=0时等价于数组只有一个元素, 即只有一个根节点, 而无子树 45 { 46 int temp = arr[0]; 47 arr[0] = arr[j]; 48 arr[j] = temp; 49 HeapAdjust(arr, 0, j); 50 } 51 }