一、异或门
1. 功能叙述
两个输入信号为相反电平时,输出才为高电平
2. 符号
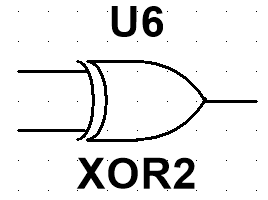
- 计算机符号:XOR
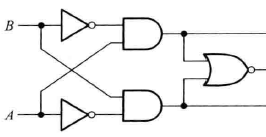
3. 组成基本逻辑
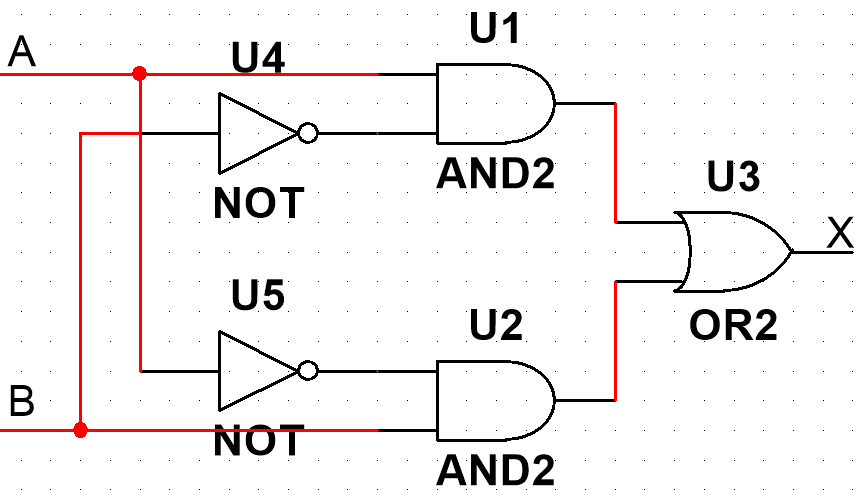
4. 逻辑表达式
※ X=AB'+A'B=A⊕B
5. 真值表
| A | B | X |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
6. 实例应用
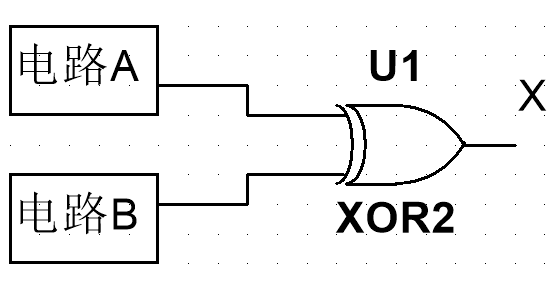
- 功能叙述:并行工作的两个相同电路,只要这两个电路工作正常,则输出总是相同的,则异或门输出为低电平,只要有其中一个出了问题,则输出为高电平。用于指示其中一个电路出现了异常
- 局限性:如果两个电路同时出现故障,但出现的故障相同,产生的错误输出相同,则异或门无法检测出电路错误
7. 引申到同或门
与异或门相反,两个输入信号为相同电平时,输出才为高电平
X=AB+A'B'=(A⊕B)'
二、 用异或门组成半加器
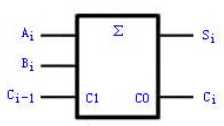
1. 半加器构造:

A:输入端1
B:输入端2
S:求和原位(∑)
C:进位
举例 :
- 1+1=10,(A=1,B=1,S=0,C=1)
- 1+0=01, (A=1,B=0,S=0,C=0)
- 0+0=00, (A=0,B=0,S=0,C=0)
2. 真值表
| A | B | S(∑) | C |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 |
3. 内部原理叙述
由真值表我们分类讨论
S(∑)=A⊕B
C=A+B
则我们可以画出内部构造:

三、 用异或门组成全加器
1. 全加器构造
2. 进阶与区分
- 与半加器的区别:半加器只能处理1位二进制数,而全加器不仅能处理本位的进位,还可以处理地一位的进位。请带着这个结论看下列的真值表找寻规律
3. 真值表
|
输入
|
输出
|
|||
|
Ci-1
|
Ai
|
Bi
|
Si
|
Ci
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
1
|
1
|
1
|
4. 原理解释(规律解释)
- 全加器必须将两个输入位和一个进位输入位相加
(1)详细说明
(╯3╰)以真值表倒数第3行为例子,输入为B=1,A=0,本位输出按照半加器应该是为1,但是Ci-1=1意味着本位的上一位(低一位)进位了一个1上来,所以
(高一位进位0)(本位1)+(低一位进位1)=(高一位进位1)(本位0)(低一位)
( 0 10 )+ ( 010 )= 1 0 0
简单来说:即(010+000)+(001+001)=100
( B + A )+ (低位进1) =100
(╯3╰)以真值表倒数第1行为例子,输入为B=1,A=1,本位输出按照半加器应该是为0,向前一位进位1,但是Ci-1=1意味着本位的上一位(低一位)进位了一个1上来,所以
(高一位进位1)(本位0)+(低一位进位1)=(高一位进位1)(本位0)(低一位)
( 1 00 )+ ( 10 )= 1 1 0
简单来说:即(010+010)+(001+001)=100
( B + A )+ (低位进1) =110
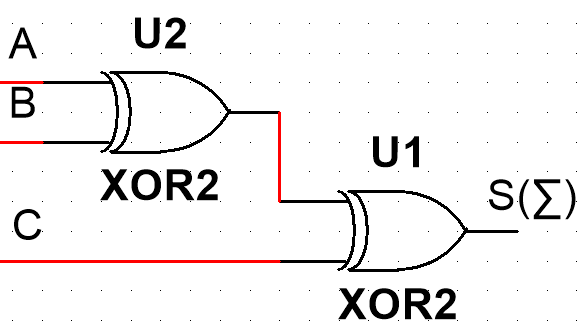
(2)进一步剖析逻辑门:关于输出Si
A, B, Cin进位相加
∑(Si) = ( A ⊕ B ) ⊕ C
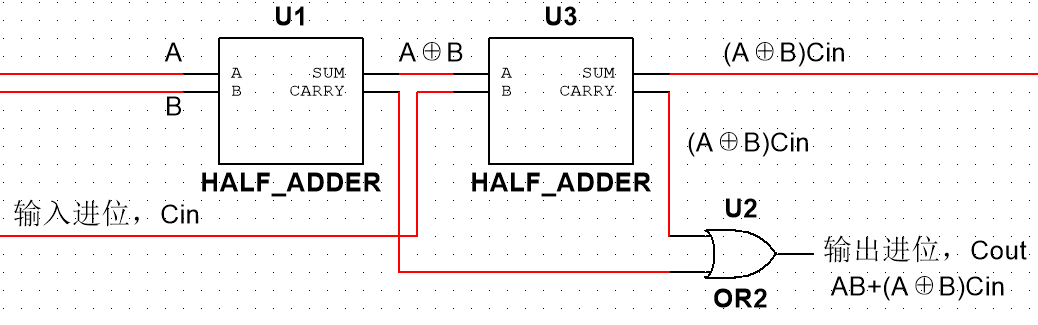
(3)进一步剖析逻辑门:关于输出Ci
Cout=AB+(A⊕B)Cin

Ci即为Cout, Ci-1即为Cin. ( i 指的是当前位数
5. 两个半加器组成全加器
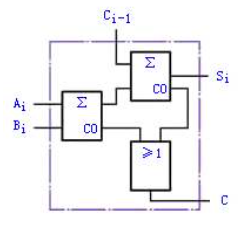
四、 并行加法器
- 将加法器组合在一起 形成并行二进制加法器
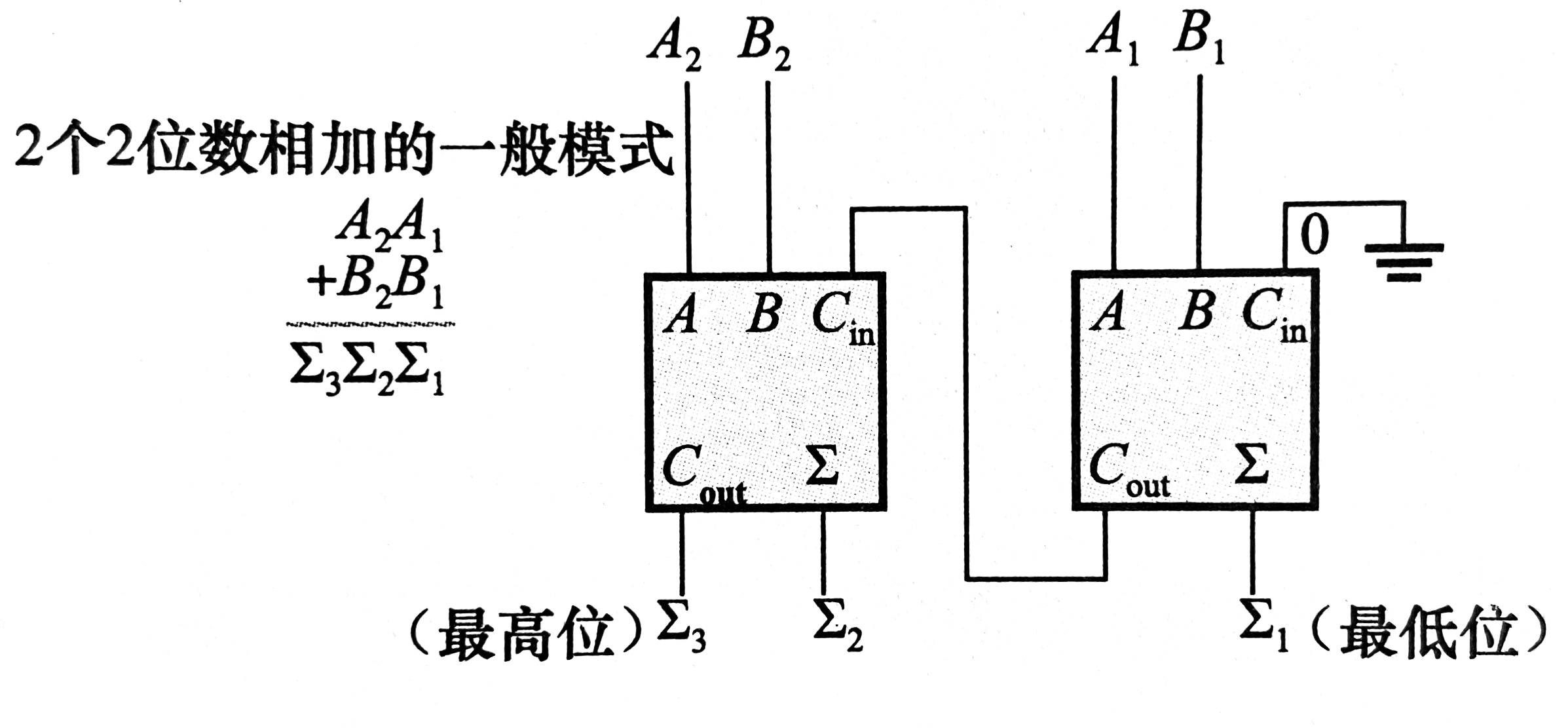
1. 二位并行加法器
- 下图中,用A1、B1表示两个数字得到最低有效位(LSB)。A2、B2来表示相邻的高位,∑1、∑2、∑3表示三个和位,注意,最左边全加器的进位输出变为和中的最高有效位(MSB)∑3
2. 四位并行加法器(类推)
- 将四位作为一组称为半字节
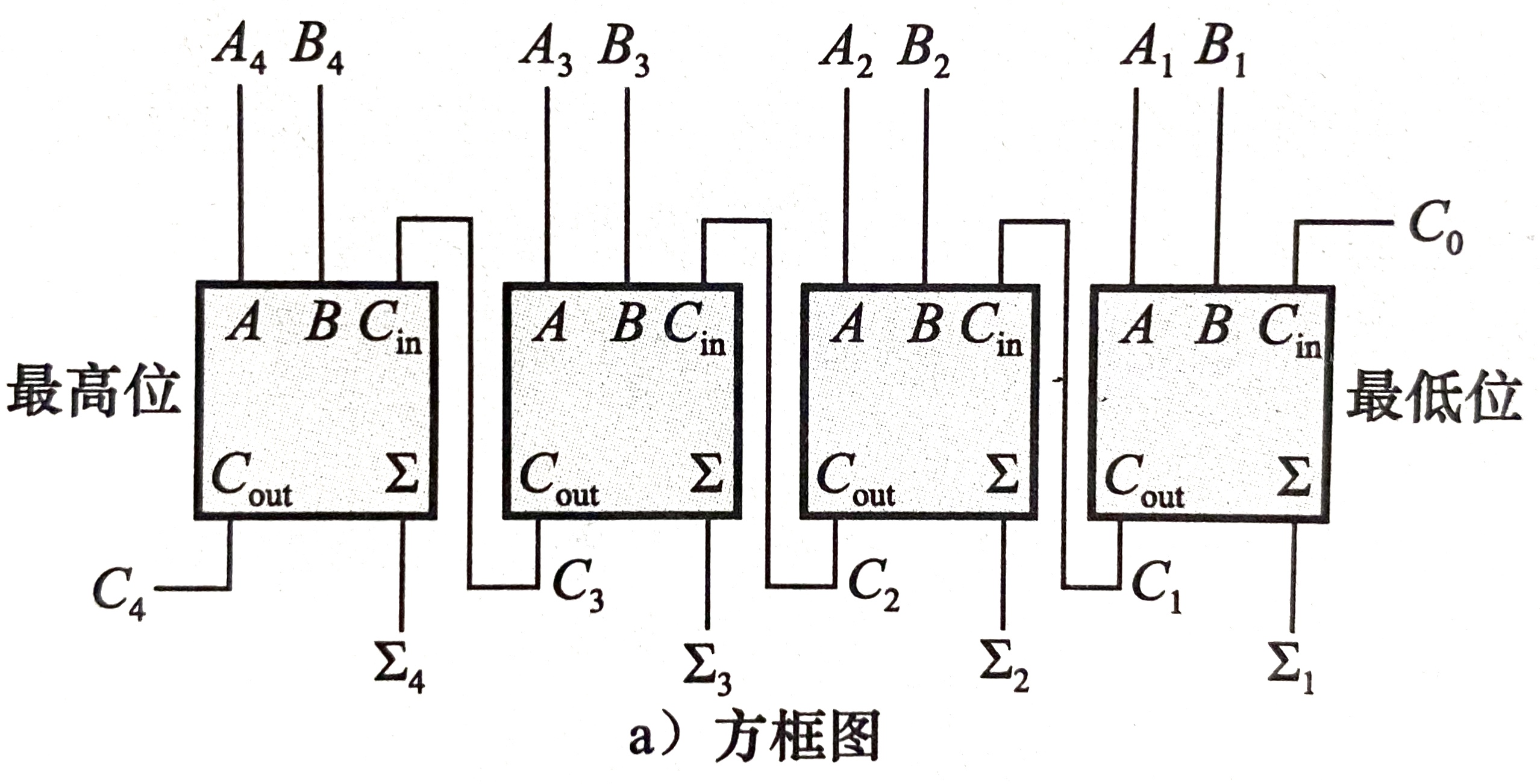
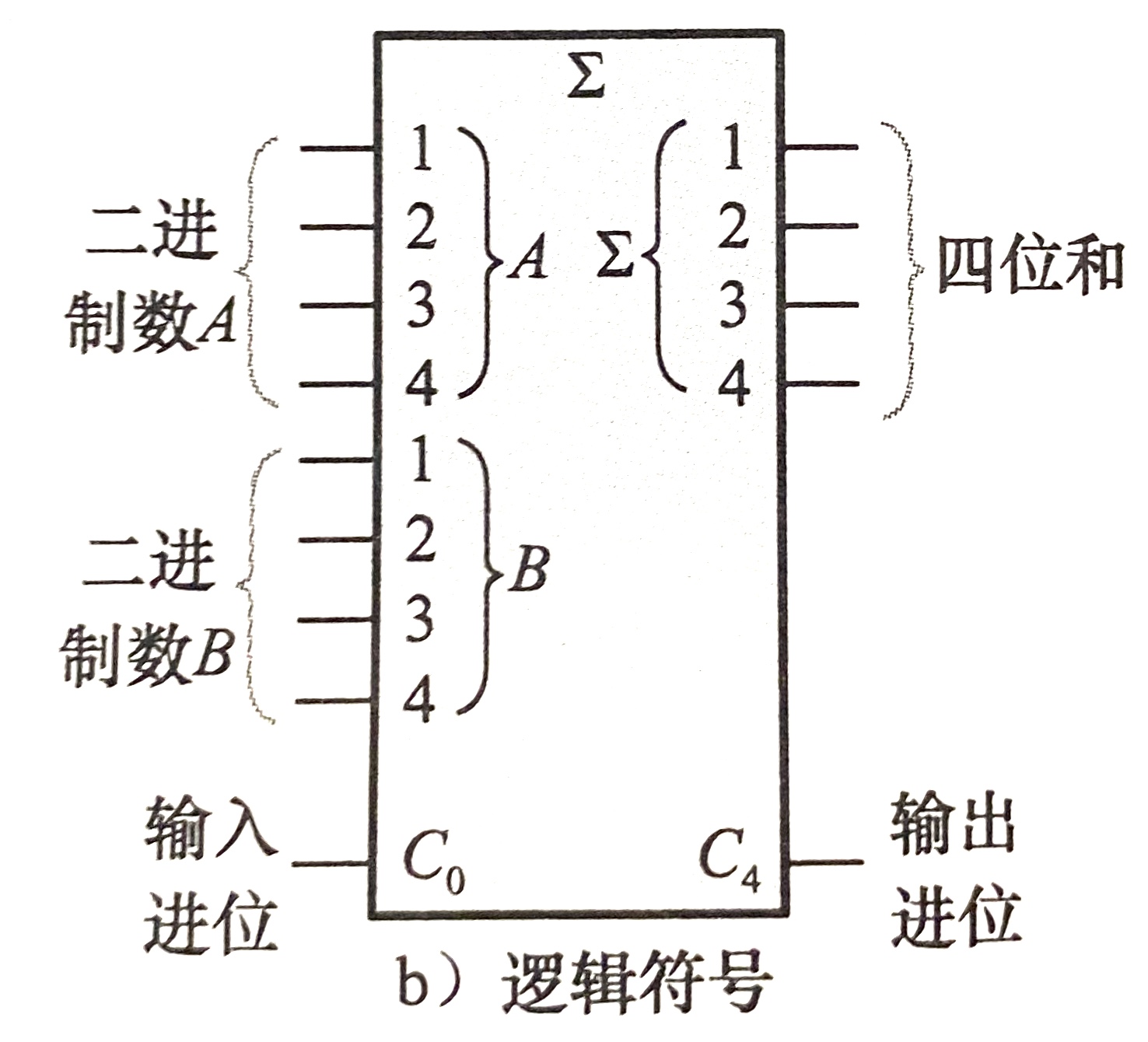
3. 串行进位与超前进位加法器
(1)串行进位
- 每一个全加器的进位输出连接到下一个高一级的全加器的输入(一级对应一个全加器)
- 任何一级的输出和及进位必须在上一级的进位到来后才能产生,这将出现时间延迟
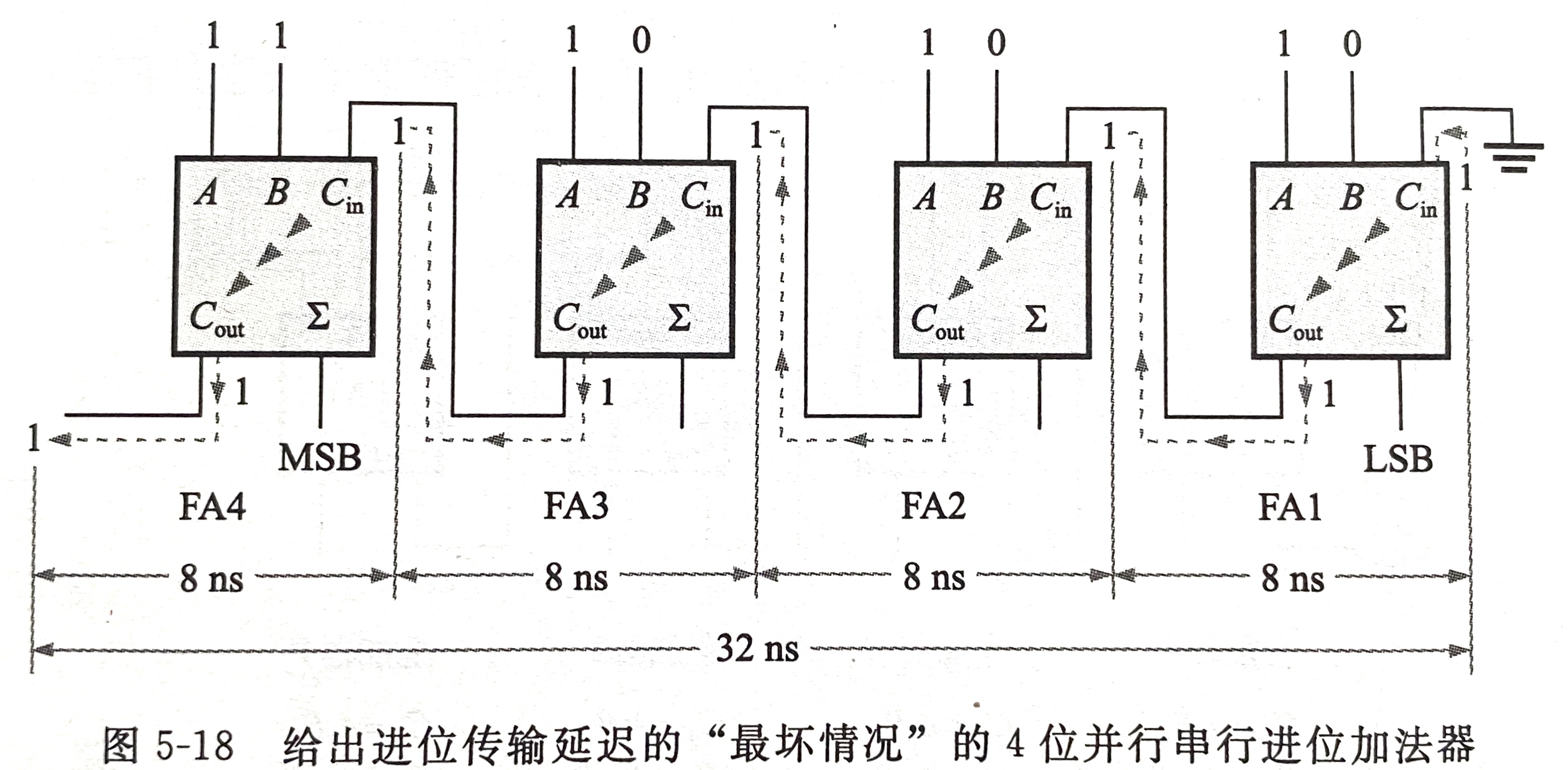
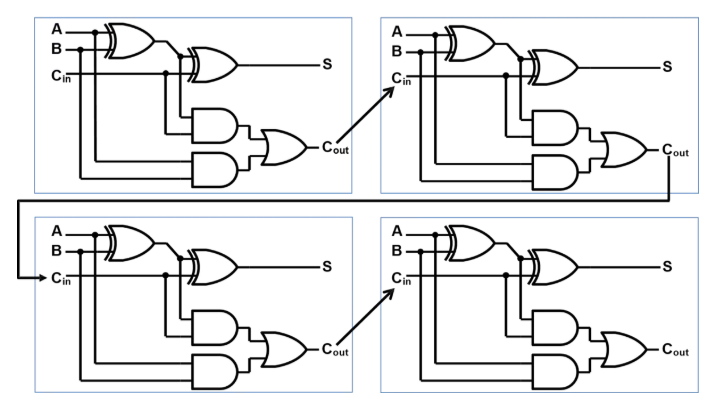
这样进位输出,像波浪一样,依次从低位到高位传递, 最终产生结果的加法器,也因此得名为行波进位加法器(Ripple-Carry Adder,RCA)
- 延迟时间计算:
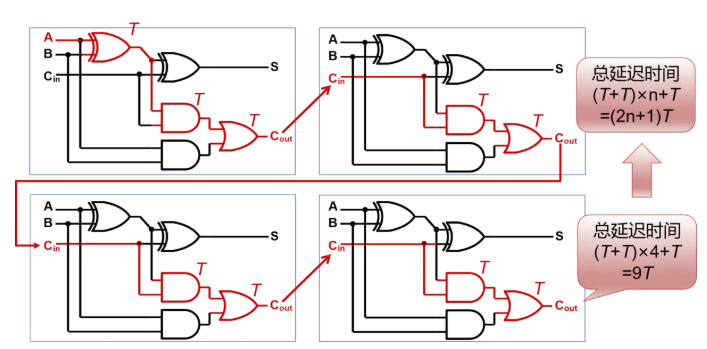
对于最低位的全加器,它在A、B和Cin都已经准备好。其实,输入信号进入到这块电路之后,在连接线上传递需要花时间。 称为线延迟,而经过这样的门,也需要花时间,称为门延迟。 在进行设计原理分析时,我们主要关注门延迟。
从第一个全加器的A-S这条通路来看,产生第一个S输出,需要通过两个门的延迟。 所以它显然不是最长的路径,当然,从A出发或着从B出发都是一样的, 所以对于第一个全加器,它的最长路径,是红色线标记的那条,后面的全加器关键路径同理可得。那么,假设经过一个门电路的延迟时间为T,那么经过4个全加器所需要的总延迟时间就是:2T x 4 + T(第一个全加器产生3个T) = 9T。所以推出,经过n个全加器所产生的总延迟时间为2T x n + T = (2n+1)T。
(2)超前进位加法器
第一种超前进位加法器推导方法
产生进位信号:出现在全加器内部加法运算产生的进位输出的时刻。当且仅当两个输入为1时,生成一个产生进位信号。产生进位函数Cg用两个输入位A和B的与运算表示。Cg=AB
传送进位信号:出现在输入进位串行传送到输出进位的时刻。当全加器额的输入位只要有一个位为1时,输入进位便可通过全加器进行传送。传送进位函数Cp用两个输入位的或运算表示Cp=A+B
(当Ai,Bi,Ci有任意两个输入为1时,Ci+1就为1)

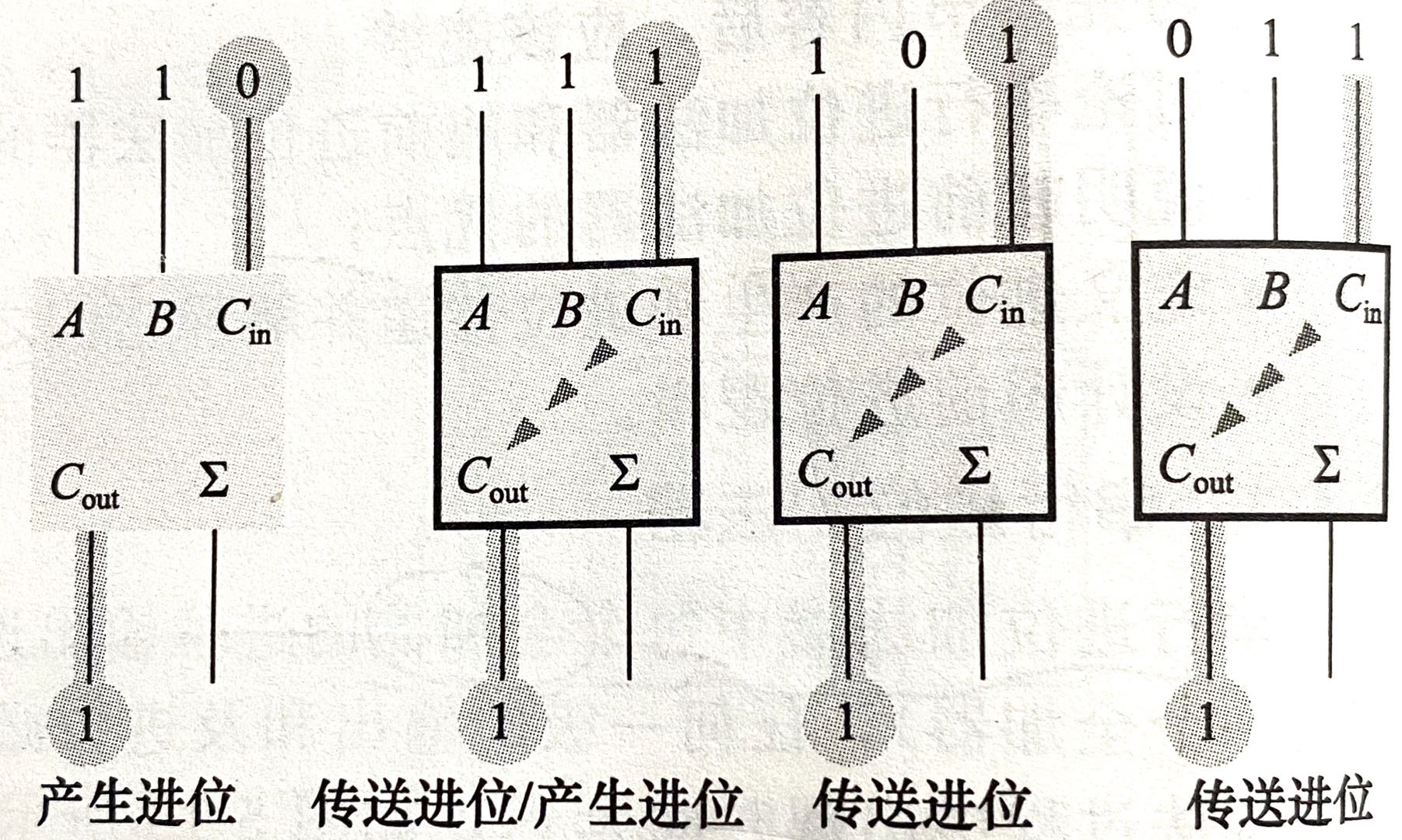
当Ai和Bi都为1时,Gi = 1,产生进位Ci+1 = 1
当Ai和Bi有一个为1时,Pi = 1,传递进位Ci+1 = Ci
因此Gi 定义为进位产生信号,Pi定义为进位传递信号。Gi的优先级比Pi高,也就是说:当Gi = 1时(当然此时也有 Pi = 1 ),无条件产生进位,而不管Ci是多少;
当Gi=0而Pi=1时,进位输出为Ci, 跟Ci之前的逻辑有关。
由此来表示4个全加器的进位输出为:

根据上面的优化算法,我们重新绘制了CLA的布线方式:

延迟计算:
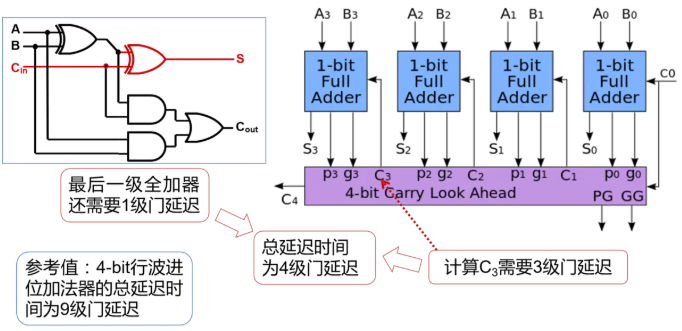
最后四位超前进位加法运算器的逻辑图如下:

第二种超前加法进位器推导方法(下面这个链接讲的很清楚)
https://zhuanlan.zhihu.com/p/101332501
五. 比较器(以同或门为核心)
(1)基本功能
比较两个二进制数的大小以确定这两个量的关系
(2)相等比较器
由于串行进位加法器的速度受到进位信号的限制,人们又设计了一种多位数超前进位加法逻辑电路,使每位的进位只由被加数和加数决定,而与低位的进位无关
(3)不等比较器
略