题目:传送门
题意

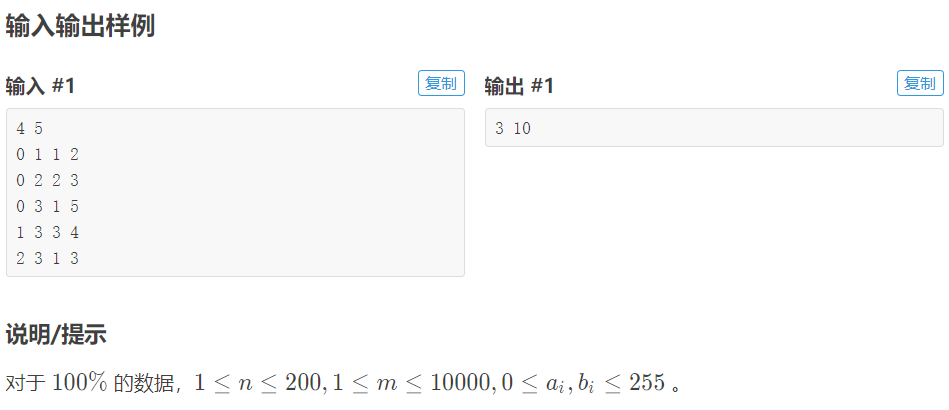
思路
将每条边的 a 和 b 看成二维坐标系上的点 (a,b),然后找到这些点中距离 y 轴最近的点(即 x 最小的点) A 和 距离 x 轴最近的点 B(y最小的那个点)。也就是现在我们知道了两个方案 A 和 B,假设现在有一个更优的方案 C,那么 C 在二维坐标系上,要满足在向量 AB 的右边。然后我们接着递归 AC, CB 直到不存在点在 AB 的右边。
#include <bits/stdc++.h> #define LL long long #define ULL unsigned long long #define mem(i, j) memset(i, j, sizeof(i)) #define rep(i, j, k) for(int i = j; i <= k; i++) #define dep(i, j, k) for(int i = k; i >= j; i--) #define pb push_back #define make make_pair #define INF 0x3f3f3f3f #define inf LLONG_MAX #define PI acos(-1) #define fir first #define sec second #define lb(x) ((x) & (-(x))) using namespace std; const int N = 2e6 + 5; int f[N]; struct note { int u, v; LL a, b, c; } a[N]; bool cmp(note a, note b) { return a.c < b.c; } pair < LL, LL > ans; LL ANS = inf; int n, m; int Fin(int v) { if(f[v] == v) return v; return f[v] = Fin(f[v]); } pair < LL, LL > get() { /// 最小生成树 rep(i, 1, n) f[i] = i; sort(a + 1, a + 1 + m, cmp); pair < LL , LL > res = make(0, 0); rep(i, 1, m) { if(Fin(a[i].u) == Fin(a[i].v)) continue; res.fir += a[i].a; res.sec += a[i].b; f[Fin(a[i].u)] = Fin(a[i].v); } if(res.fir * res.sec < ANS || (res.fir * res.sec == ANS && res.fir < ans.fir)) ans = res, ANS = res.fir * res.sec; return res; } void cal(pair < LL, LL > A, pair < LL, LL > B) { rep(i, 1, m) a[i].c = (B.fir - A.fir) * a[i].b + (A.sec - B.sec) * a[i].a; pair < LL, LL > C = get(); if((B.fir - A.fir) * (C.sec - A.sec) - (B.sec - A.sec) * (C.fir - A.fir) >= 0) return ; cal(A, C); cal(C, B); } int main() { scanf("%d %d", &n, &m); rep(i, 1, m) { scanf("%d %d %lld %lld", &a[i].u, &a[i].v, &a[i].a, &a[i].b); a[i].u++; a[i].v++; } rep(i, 1, m) a[i].c = a[i].a; pair < LL, LL > A = get(); rep(i, 1, m) a[i].c = a[i].b; pair < LL, LL > B = get(); cal(A, B); printf("%lld %lld ", ans.fir, ans.sec); return 0; }