所谓样条曲线是指给定一组控制点而得到一条曲线,曲线的大致形状由这些点予以控制,一般可分为插值样条和逼近样条两种,插值样条通常用于数字化绘图或动画的设计,逼近样条一般用来构造物体的表面。CatmullRom样条与上一节所讲的B样条很相似,不同在于CatmullRom样条的曲线会经过其每一个控制点。
The centripetal Catmull–Rom is a subclass of cubic Hermite spline that extends the Catmull–Rom implementation by allowing each of the four control points to be associated with an arbitrary time interval in the computation of a value on the curve. This modifies the behavior of the curve. The curve is an interpolation, and will intersect with all but the first and last control points. If the time intervals are uniform, the result will be the same as that of the original Catmull–Rom spline curve. The chordal curve uses the two dimensional Euclidean distance between control points to provide the time elements, while the centripetal curve uses the square root of the Euclidean distance. The principal reason for using the centripetal version is that it has been shown to be free of cusps and self-intersections.
关于插值与样条的介绍请看:http://www.cnblogs.com/WhyEngine/p/4020294.html
核心代码:
1 void YcCatmullRomSpline::BuildWeights() 2 { 3 ClearWeights(); 4 5 for (Yuint i = 0; i < 4; i++) 6 { 7 m_splineWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal)); 8 m_tangentWeights[i] = (Yreal*)malloc((m_subD)*sizeof(Yreal)); 9 } 10 11 Yreal u, u_2, u_3; 12 for (Yuint i = 0; i < m_subD; i++) 13 { 14 u = (float)i / m_subD; 15 u_2 = u * u; 16 u_3 = u_2 * u; 17 18 // 参见"游戏编程精粹1"P333 19 m_splineWeights[0][i] = (-1.0f*u_3 + 2.0f*u_2 - 1.0f*u + 0.0f)*0.5f; 20 m_splineWeights[1][i] = ( 3.0f*u_3 - 5.0f*u_2 + 0.0f*u + 2.0f)*0.5f; 21 m_splineWeights[2][i] = (-3.0f*u_3 + 4.0f*u_2 + 1.0f*u + 0.0f)*0.5f; 22 m_splineWeights[3][i] = ( 1.0f*u_3 - 1.0f*u_2 + 0.0f*u + 0.0f)*0.5f; 23 24 m_tangentWeights[0][i] = (-3.0f*u_2 + 4.0f*u - 1.0f)*0.5f; 25 m_tangentWeights[1][i] = ( 9.0f*u_2 - 10.0f*u + 0.0f)*0.5f; 26 m_tangentWeights[2][i] = (-9.0f*u_2 + 8.0f*u + 1.0f)*0.5f; 27 m_tangentWeights[3][i] = ( 3.0f*u_2 - 2.0f*u + 0.0f)*0.5f; 28 } 29 }
切图:
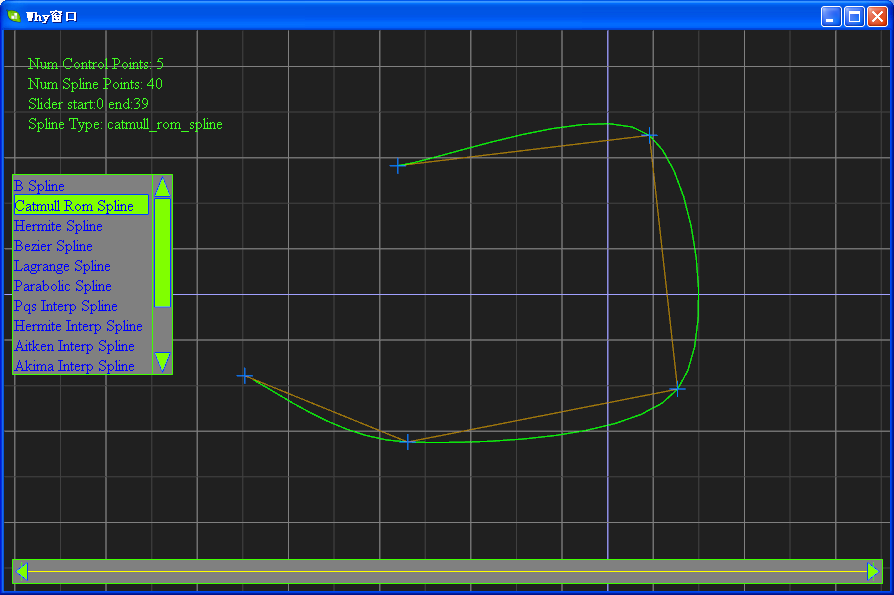

相关软件的下载地址为:http://files.cnblogs.com/WhyEngine/TestSpline.zip