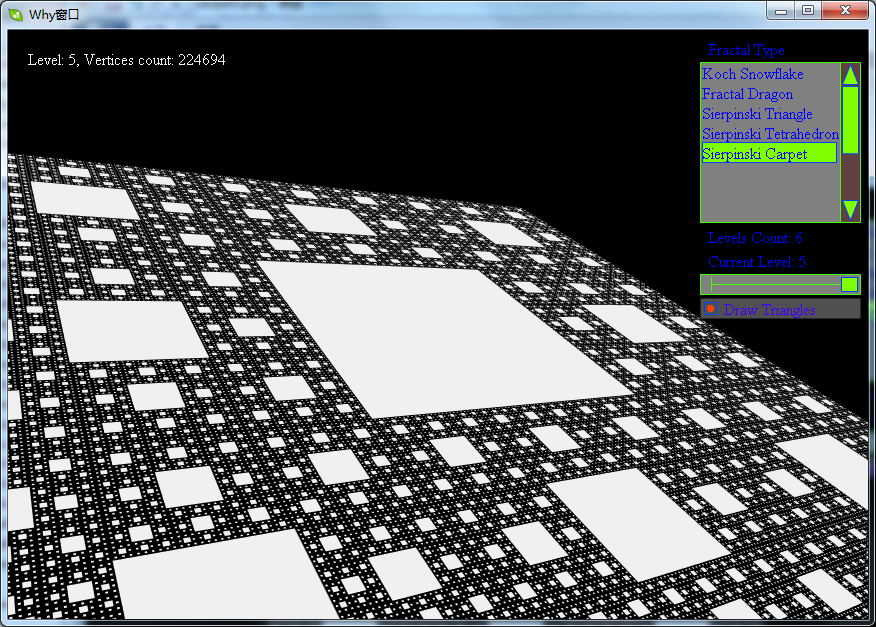
前面讲了谢尔宾斯基三角形,和这一节的将把三角形变为正方形,即谢尔宾斯基地毯,它是由瓦茨瓦夫·谢尔宾斯基于1916年提出的一种分形,是自相似集的一种。
谢尔宾斯基地毯的构造与谢尔宾斯基三角形相似,区别仅在于谢尔宾斯基地毯是以正方形而非等边三角形为基础的。将一个实心正方形划分为的9个小正方形,去掉中间的小正方形,再对余下的小正方形重复这一操作便能得到谢尔宾斯基地毯。如下图:
核心代码:
static void SierpinskiCarpet(const Vector3& v, Vector3* pVertices, Yreal d)
{
pVertices[0] = v + Vector3(-d, -d, 0.0f);
pVertices[1] = v + Vector3(-d, d, 0.0f);
pVertices[2] = v + Vector3( d, d, 0.0f);
pVertices[3] = v + Vector3( d, -d, 0.0f);
pVertices[4] = v + Vector3( d, 0, 0.0f);
pVertices[5] = v + Vector3(-d, 0, 0.0f);
pVertices[6] = v + Vector3( 0, d, 0.0f);
pVertices[7] = v + Vector3( 0, -d, 0.0f);
}