数学图形之双叶双曲面

双曲线绕其对称轴旋转而生成的曲面即为双曲面,上节讲了单叶双曲面,这一节继续讲双叶双曲面.

双叶双曲面的数学公式如下:

x*x/a/a + y*y/b/b - z*z/c/c = -1

在数学里，双曲面是一种二次曲面。采用直角坐标 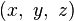 ，双曲面可以用公式表达为

  （单叶双曲面），

或

  （双叶双曲面）。

假若， ，则称为旋转双曲面。

本文将展示几种生成双叶双曲面算法和切图.使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.QQ交流群: 367752815

(1)

#x*x/a/a + y*y/b/b - z*z/c/c = -1

vertices = dimension1:72 dimension2:72

u = from 0 to (2*PI) dimension1
v = from (-5) to (5) dimension2 

a = rand2(1, 5)
b = rand2(1, 5)
c = rand2(1, 5)

x = a*sqrt(v*v - 1)*cos(u)
z = b*sqrt(v*v - 1)*sin(u)
y = c*v

(2)

vertices = D1:100 D2:100
u = from 0 to (1*PI) D1
v = from (0) to (2*PI) D2 gap[PI*0.5, PI*1.5]
a = rand2(1, 10)
b = rand2(1, 10)
c = rand2(1, 10)
x = a*tan(v)*sin(u)
y = b*sec(v)
z = c*tan(v)*cos(u)

(3)

我之前写过关于双曲线的文章,数学图形(1.10) 双曲线

将双曲线旋转一周即能生成双曲面.

vertices = 360
u = from -1 to 1 gap[0]

x = u
y = 1/x

y = limit(y, -50, 50)

surface_slices = 72
rotate = anchor[0, 0, 0], axis[1, 1, 0], angle[0, 2*PI]

(4)

双曲面(东西开口)

vertices = 100

t = from 0 to (2*PI) gap[PI*0.5, PI, PI*1.5]
a = rand2(0.1, 10)
b = rand2(0.1, 10)

x = a*sec(t)
y = b*tan(t)

x = limit(x, -50, 50)
y = limit(y, -50, 50)

surface_slices = 72
rotate = anchor[0, 0, 0], axis[1, 0, 0], angle[0, 2*PI]

双曲面(南北开口)

vertices = 100

t = from 0 to (2*PI) gap[PI*0.5, PI, PI*1.5]
a = rand2(0.1, 10)
b = rand2(0.1, 10)

x = a*tan(t)
y = b*sec(t)

x = limit(x, -50, 50)
y = limit(y, -50, 50)

surface_slices = 72
rotate = anchor[0, 0, 0], axis[0, 1, 0], angle[0, 2*PI]