数学图形之常用函数

      如果你也像我一样毕业多年,你是否还记得当年所学的数学中那些函数:幂,对数,指数,正弦,余弦,正切,余切,反正弦,反余弦,反正切,反余切,双曲正弦,双曲余弦,双曲正切,双曲余切,正割函数,余割函数,双曲正割,双曲正割.听这些名字让人觉得即熟悉又陌生吧.这里将展示出这些函数所生成的平面图形.你可能记得这些函数生成的是曲线,不过我这里给数据多加了一个维度,然后是以面的形式显示这些函数.怎么说这些函数的曲线样子总能通过百度或是维基上搜索到,而我这的图形可都是原创的.

      相关软件参见:数学图形可视化工具

(1)幂函数

X的N次幂.

vertices = D1:100 D2:100

u = from (-2) to (2) D1
v = from 0 to 4 D2

x = u
y = v*pow_sign(u, v)

脚本代码中X,N都为变量,两个变量会生成一个二维数据,得到一个平面图形.pow_sign是一个保留正负号的pow函数,其C++实现为:

static float     yf_pow_sign(float a, float b)
{
    float s = yf_sign(a);
    a = ::fabsf(a);
    if (a < FLT_EPSILON)
    {
        return 0.0f;
    }
    return ::powf(a, b)*s;
}

上图为脚本所生成的图形,右下角有两个滑动块控件,在软件中按下键盘'P'会出现,用于设置当前选择的数值.图形上的红色曲线表示当前数值下的函数曲线.

(2)指数函数

它与幂函数很相似,表示N的X次幂

vertices = D1:100 D2:100

u = from (-10) to (10) D1
v = from 0.1 to 10 D2

x = u
y = pow_sign(v, u)

y = limit(y, -50, 50)

脚本中y = limit(y, -50, 50)表示将Y值限定在-50到50之间,以防止图形过大.

(3)对数函数

对数函数与指数函数相对应

vertices = D1:100 D2:100

u = from 0.1 to 10 D1
v = from 1 to 10 D2

x = u
y = log_ax(v, u)

y = limit(y, -50, 50)

图中有一条红色曲线,一条绿线,按下键盘'8'会显示在右上角的面板.其中会显示两线交点的数值信息

(4)log函数

vertices = D1:360 D2:100
u = from (0.001) to (10) D1
v = from 0 to 1 D2

x = u
y = log(x)*v

v = v*2

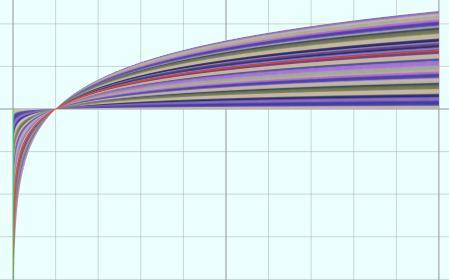
(5)pow 函数

vertices = D1:360 D2:100
u = from 0 to 1 D1
v = from 0.1 to 10 D2
s = 10
x = s*u
y = s*pow(u, v)

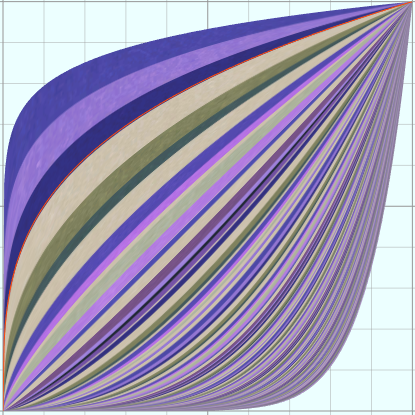
(6)EXP

vertices = D1:360 D2:100
u = from (-4) to (4) D1
v = from 0 to 1 D2

x = u
y = exp(x)*v

v = v*2

(7)正弦

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = v*sin(u)

u = u*5
v = v*2

 

(8)余弦

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = v*cos(u)

u = u*5
v = v*2

 

(9)正切

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = tan(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

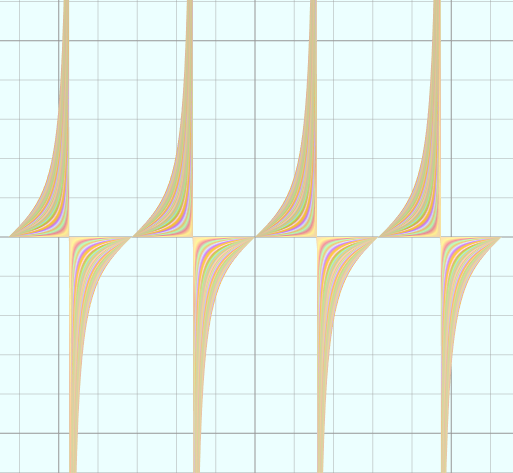
(10)余切

vertices = D1:360 D2:100
u = from (-4*PI) to (4*PI) D1
v = from 0 to 1 D2

x = u
y = cot(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

(11)反正弦

vertices = D1:360 D2:100
u = from (-1) to (1) D1
v = from 0 to 1 D2

x = u
y = asin(x)*v

v = v*2

 

(12)反余弦

vertices = D1:360 D2:100
u = from (-1) to (1) D1
v = from 0 to 1 D2

x = u
y = acos(x)*v

v = v*2

 

(13)反正切

vertices = D1:360 D2:100
u = from (-10) to (10) D1
v = from 0 to 1 D2

x = u
y = atan(x)*v

v = v*2

 

vertices = D1:360 D2:100
u = from (-10) to (10) D1
v = from -10 to 10 D2

x = u
y = atan2(u, v)

 

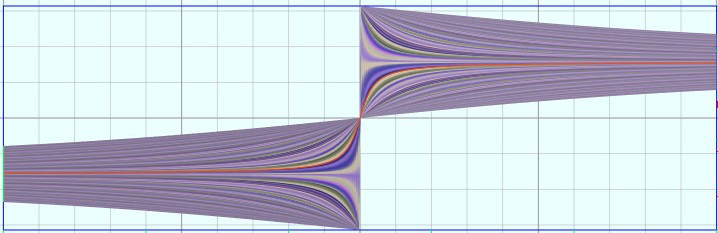
(14)反余切

vertices = D1:360 D2:100
u = from (-10) to (10) D1
v = from 0 to 1 D2

x = u
y = acot(x)*v

v = v*2

 

(15)双曲正弦

vertices = D1:360 D2:100
u = from (-0.9*PI) to (0.9*PI) D1
v = from 0 to 1 D2

x = u
y = sinh(x)*v

u = u*5
v = v*5

 

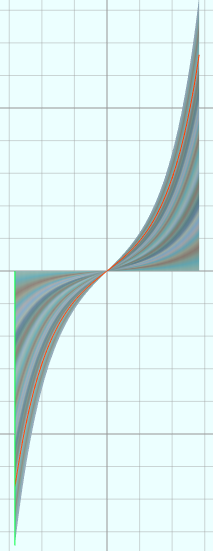
(16)双曲余弦

vertices = D1:360 D2:100
u = from (-0.9*PI) to (0.9*PI) D1
v = from -1 to 1 D2

x = u
y = cosh(x)*v

u = u*5
v = v*5

 

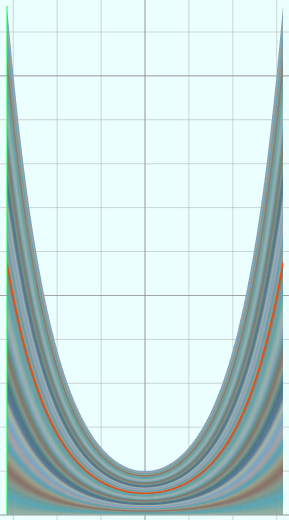
(17)双曲正切

vertices = D1:360 D2:100
u = from (-0.9*PI) to (0.9*PI) D1
v = from -1 to 1 D2

x = u
y = tanh(x)*v

u = u*5
v = v*5

 

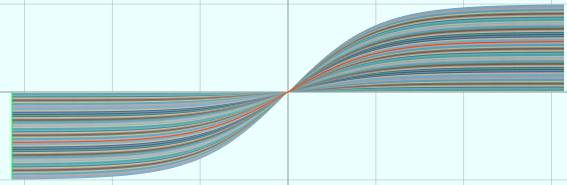
(18)双曲余切

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = cth(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

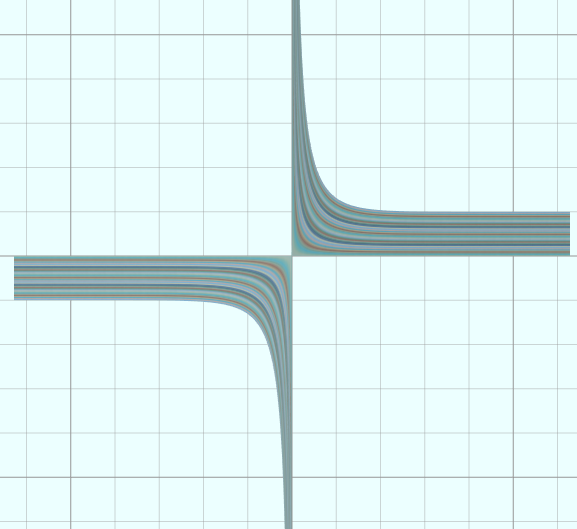
(19)正割函数

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = sec(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

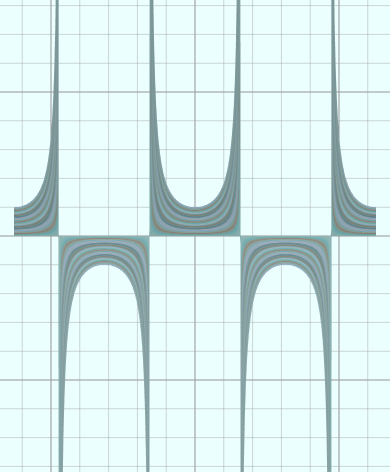
(20)余割函数

vertices = D1:360 D2:100
u = from (-2*PI) to (2*PI) D1
v = from 0 to 1 D2

x = u
y = csc(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

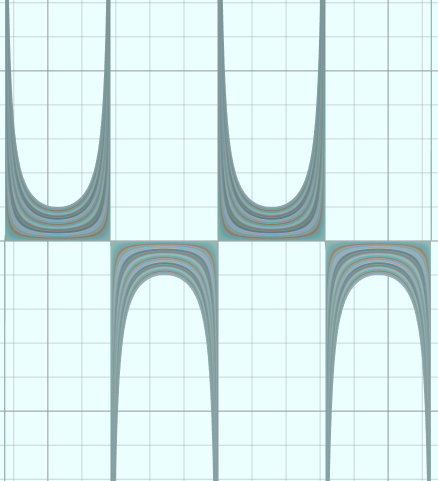
(21)双曲正割

vertices = D1:360 D2:100
u = from (-PI) to (PI) D1
v = from -1 to 1 D2

x = u
y = sch(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

(22)双曲余割

vertices = D1:360 D2:100
u = from (-PI) to (PI) D1
v = from -1 to 1 D2

x = u
y = xh(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5

 

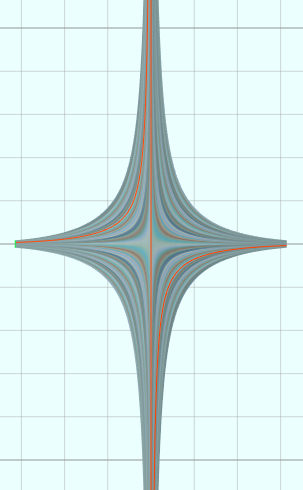
(23)反正割

vertices = D1:360 D2:100
u = from (-10) to (10) D1
v = from 0 to 1 D2

x = u
y = asec(x)*v + PI/2*(1 - v)

y = limit(y, -100, 100)

u = u*5
v = v*5

(24)反余割

vertices = D1:360 D2:100
u = from (-10) to (10) D1
v = from 0 to 1 D2

x = u
y = acsc(x)*v

y = limit(y, -100, 100)

u = u*5
v = v*5